Действительные функции

Основные определения, связанные с понятием «функция», были даны в п. 2.12 пособия [1]. В математическом анализе изучают так называемые действительные функции и их различные обобщения; у действительной функции
f: Х ®U множества Х и Y суть подмножества множества действительных чисел R. Важным частным случаем понятия действительной функции является понятие последовательности.

Последовательностью элементов числового множества Х называется функция f, определенная на множестве натуральных чисел N и принимающая значения в множестве Х, т.е. f: N ® Х. Элементом или членом последовательности f называется упорядоченная пара (п, х), х=f (п), п Î N, хÎ Х; натуральное число п называется номером элемента последовательности, а число хÎ Х – его значением.

Последовательность f: N ® Х традиционно принято обозначать как {x_n}, п=1, 2, ¼.

Стационарная последовательность определяется как x_n = а для всех n=1,2,¼.

Конечная последовательность задается как отображение начального отрезка натурального ряда {1, 2, ¼, n} в множество Х.

Последовательность может задаваться:

1) формулой ее общего члена, зависящей от номера n, например, x_n=5ⁿ ;

2) рекуррентной формулой, например,

3) словесным описанием, например: последовательность логарифмов по основанию 2 от всех простых натуральных чисел в порядке их возрастания.

Последовательность {x_n} называется ограниченной сверху (снизу), если существует число S (s), большее (меньшее) любого ее члена, т.е. "n х_n < S ("n x_n >s). Если последовательность {x_n} ограничена и сверху, и снизу, то она называется ограниченной.

Последовательность {x_n} называется бесконечно большой (бесконечно малой), если для любого положительного числа e существует номер N такой, что при всех n > N выполняется условие |x_n| > e (|x_n| < e).

Формальная запись: "e $N "n n>N Þ |x_n| > e (|x_n| < e).

Пример 1.1.

1) Последовательность x_n = - n ограничена сверху, поскольку для S = 0 имеем очевидное неравенство 0 > - n при п = 1, 2, …; но эта последовательность не ограничена снизу. Напротив, последовательность х_п = log₂ п ограничена снизу, поскольку для s = -1, очевидно, log₂n > - 1 при п = 1, 2, …; в то же время она не ограничена сверху.

2) Последовательность x_n = ограничена, т.к. для S = 2 и s = 0 выполняются очевидные неравенства 2 > > 0 при n = 1, 2, ….

3) Последовательность х_п = п бесконечно большая, а последовательность х_п = –- бесконечно малаяn

ПРЕДЕЛ

Содержательно понятие предела означает, что переменная величина, зависящая от другой переменной величины, изменяющейся определенным образом, неограниченно близко приближается к определенному постоянному значению. С пределом, или предельным переходом, связаны фундаментальные понятия математического анализа: непрерывность, производная, интеграл и др. Простейшим случаем предела является предел последовательности действительных чисел.

Последовательность действительных чисел {x_n} называется сходящейся к числу А, если для любого e > 0 существует такое натуральное число N, что для всех n > N выполняется условие 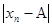< e.

Формальная запись: "e $N "n n>N Þ |x_n - A| < e.

При этом говорят также, что число А является пределом данной последовательности и пишут

или .

Если последовательность не является сходящейся, ее называют расходящейся.

Если последовательность {x_n} бесконечно большая (а следовательно, расходящаяся), то условно пишут ; если при этом, начиная с некоторого номера N, все элементы положительны (отрицательны), то условно пишут . Условность этих обозначений в том, что ни ¥, ни ± ¥ числами не являются. Для бесконечно малой последовательности, очевидно, .

Для сходящихся последовательностей справедливы следующие утверждения:

1) Если x_n = a, n = 1, 2, … (стационарная последовательность), то .

2) Сходящаяся последовательность ограничена.

3) Если 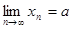, , то

4) ;

5) ;

6) (при b ¹ 0).

7) Если и х_n £ z_n £ y_n, то .

Пример 1.2.

1)

2) ; ;

3)

4) n

Последовательность {x_n} называется возрастающей (убывающей), если х₁ < х₂ < … < х_n < x_n+1 < …(x₁ > x₂ >…>x_n > x_n+1 >…); неубывающей (невозрастающей), если х₁ £ х₂ £ … £ х_n £ x_n+1 £ …(x₁ ³ x₂ ³…³x_n ³ x_n+1 ³…).

Формальная запись: "i"j i>j Þ x_i>x_j ("i"j i>j Þ x_i<x_j)

Все такие последовательности называются монотонными; возрастающие и убывающие называются при этом строго монотонными.

Любая монотонная ограниченная последовательность имеет предел. Примером ограниченной монотонно возрастающей последовательности является последовательность . Ее пределом служит число e, e; это иррациональное число, приближенно равное 2,71828. Его называют также основанием натуральных логарифмов и пишут log_ex = lnx.

С помощью понятия предела последовательности определяются другие понятия предела, например, предела функции.

Рассмотрим действительную функцию f: Х ®U. Для функции f существует предел А в точке x_о, х_о Î Х, если для любой сходящейся к х₀ последовательности {x_n}, существует предел последовательности значений функции не зависящий от выбора последовательности {x_n} и равный А. Предел функции обозначают .

Критерий Коши существования предела функции. Если для любого e > 0 существует d =d(e) > 0 такое, что для всех хÎХ, таких что |х₀ – х|< d (e), выполняется условие

| A - f(x)| < e

(формальная запись: "e $d(e) "x |х₀ – х|< d (e) Þ | A - f(x)| < e),

то т.е. число А является пределом функции f в точке х₀ в смысле первоначального определения через произвольные сходящиеся к х₀ последовательности {x_n}. n

Множество {x: |x₀ – x| < d} называют d - окрестностью точки х₀

Определенный выше предел функции f называют двусторонним; существуют понятия односторонних пределов слева и справа.

Число А⁺ (А^-) называется односторонним пределом справа (слева) функции f в точке х_0, что обозначается (), если члены последовательности {x_n} принадлежат множеству {x| x ³ x₀} ({x| x £ x₀}), т.е. если для любой последовательности {x_n}, сходящейся к х₀ и такой, что x_n ³ x₀ (х_n £ x₀) для любого n = 1, 2, ¼, выполняется условие

Если А⁺ = А^-, то существует и двусторонний предел А, причем А⁺ = А^- =А.

Критерий Коши существования односторонних пределов предлагаем сформулировать в качестве упражнения.

Пример 1.3.

Рассмотрим функцию f(х) = sign (x), определяемую как

Ясно, что в точке х₀=0 существуют левосторонний предел , правосторонний предел причем они не равны, т.е. в х₀ = 0 не существует двустороннего предела. n

Для пределов функций справедливы следующие соотношения:

1) для любых действительных чисел с₁, с₂;

2) для функции-константы (f(x) º c)

3)

4) если 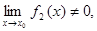то

5) если на Х, то

Функцию f(x) называют бесконечно малой в точке х₀, если Ясно, что функция f(x) имеет предел А в точке х₀ тогда и только тогда, когда функция g(x) = f(x) – A является бесконечно малой в точке х₀.

Функцию f(x) называют бесконечно большой в точке х₀, если для любого числа e > 0 и любой последовательности {x_n}, сходящейся к х₀, существует такое натуральное число N, что для всех n > N | f(x_n)|> e.

Формальная запись: "e $N "n n>N Þ | f(x_n)|> e

Если функция f(xn) бесконечно большая в точке х0, то условно пишут 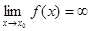и говорят в этом случае о бесконечном пределе функции. Условность этого обозначения, как и соответствующего термина, связана с тем, что символ ¥ не является числом (см. аналогичные обозначения для бесконечно больших последовательностей). Если для любой последовательности {xn}, сходящейся к х0, и любого e > 0 существует номер N, что для всех n > N f(xn)> e (f(xn) < -e), то пишут () и говорят о бесконечном положительном (отрицательном) пределе функции (формальная запись: "e $N "n n>N Þ f(xn)> e (f(xn) < -e)). Аналогичным образом вводятся обозначения для односторонних бесконечных пределов и 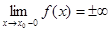с соответствующим знаком или без него.

Определение односторонних бесконечных пределов с использованием сходящихся последовательностей предлагается сформулировать читателю в качестве упражнения.

Пример 1.4.

1) Условные обозначения и используют для того, чтобы показать характер поведения гиперболы в окрестности нуля, где она ведет себя как бесконечно большая функция соответствующего знака - отрицательная при х<0 и положительная при х > 0.

2)

3) .n