Решение. 1. Найдем область определения функции. 1. Найдем область определения функции

1. Найдем область определения функции. Дробь определена, если знаменатель отличен от нуля, т. е.

; ; ; .

И так, .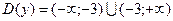

2. Найдем производную функции

3. Приравняем производную к нулю и решим уравнение ;

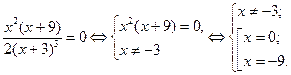
4. Найденные критические точки и точки, в которых производная не существует, отметим на числовой оси в порядке возрастания

5. Определим знаки производной на интервалах, на которые делят числовую ось критические точки и отметим полученные результаты над соответствующими интервалами;

;

;

;

.

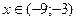
6. С учетом знака производной находим интервалы возрастания (на них производная положительная) и убывания (на них производная отрицательная). Функция возрастает при 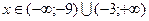и убывает при .

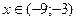7. Находим точки экстремумов функции (т. е. точки, при переходе через которые знак производной меняется на противоположный).

Поскольку при переходе через точку 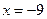первая производная меняет знак с «+» на «-», то это точка максимума:

.

Итак, − точка локального максимума.