Лема (про значення проекції на напрямок)

,

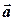де — кут між векторами та .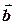

Доведення. Довести самостійно, використовуючи малюнок і геометричні міркування.

Поняття проекції вектора на напрямок іншого вектора буде потрібне при розгляді скалярного добутку векторів.

Означення (координат вектора). Пара (у випадку площини) або трійка (у випадку простору) чисел, які є проекціями даного вектора на координатні осі називаються координатами вектора (відповідно на площині і у просторі).

Теорема (про визначеність вектора своїми координатами). Кожний вектор повністю визначається парою (у випадку площини) або трійкою (у випадку простору) своїх координат; інакше кажучи, два вектори рівні тоді і тільки тоді, коли вони мають рівні відповідні координати.

(для випадку площини).

Доведення. Довести теорему самостійно. Вказівка: використати рівність прямокутних трикутників.

Теоремапро визначеність вектора своїми координатами дає підставу ототожнювати вектор з парою (у випадку площини) або трійкою (у випадку простору) його координат:

.

Безпосередньо з теореми Піфагора випливає формула для обчислення довжини вектора:

(для випадку простору).

Безпосередньо з означення координат вектора і координат точки випливає формула обчислення координат вектора при заданих координатах початку і кінця вектора: нехай і 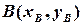довільні точки декартової площини; тоді

.

Серед усіх векторів є один вектор, який є “не зовсім” вектором, але без якого множина векторів була б логічно не повною. Ситуація щодо цього вектора дуже схожа на ситуацію з числом (нуль). Вектор, про який йдеться, так і називається: нуль-вектор. Нуль-вектор — це вектор, початок якого співпадає з його кінцем; це вектор довжини нуль; це вектор, всі координати якого дорівнюють нулю:

(для випадку простору).