Перетин двох прямих на площині; одна з прямих задана канонічним рівнянням

В тому випадку, коли одна з двох прямих ліній задана канонічним рівнянням

,

а інша загальним

,

для знаходження координат точки перетину доцільніше використовувати не правило Крамера, а параметричний спосіб розв’язання СЛР.

Пряма задана канонічним рівнянням, яке є рівністю двох дробів. Введемо змінну , яка буде величиною цих дробів:

.

Виразимо через змінні х та у:

Підставимо відповідні вирази замість х і у у рівняння другої прямої:

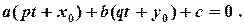
Розкриваючи дужки і зводячи подібні, отримаємо лінійне рівняння відносно однієї змінної 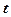. Знаходимо його розв’язок і підставляємо у вирази х і у через .

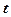Приклад. Знайдемо точку перетину двох прямих

і

.

Вводимо параметр:

.

Підставляємо вирази х і у через 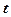в рівняння прямої :

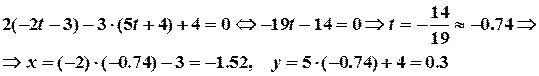
Перевірка:

Відповідь: прямі і перетинаються в точці .