Способы задания

а) Табличный. Функция может быть задана в виде таблицы.

Например, пусть температуру Т воздуха измеряют через каждый час. Тогда каждому моменту времени t= 0,l,...,24 соответствует определенное число (таблица 1):

Таблица 1

t				...
Т	Т	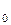T	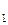Т	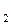...	T24

Таким образом, получена функция 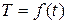, определённая на множестве целых чисел от 0 до 24, заданная таблицей. Этот способ не даёт полной характеристики функции, поскольку в таблицу часто невозможно внести все точки из области определения функции.

Например,

Таблица 2

х	–1
у

соответствует и функции и .

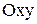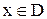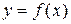б) Графический. Графиком функции называется множество точек (х,у) плоскости таких, что и . График даёт наглядное представление о характере поведения функции.

Пусть задана функция . Возьмем на плоскости систему декартовых координат XOY. Рассмотрим множество точек на плоскости , абсциссами которых являются значения аргумента 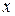, а ординатами -соответствующие значения функции 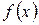. Множество 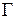называется графиком функции .

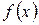Y Г

0 x

Рис. 6

Построение графика функции дополняет аналитический {или какой-нибудь другой) способ задания функции, так как делает наглядным ход ее изменения. Во многих технических устройствах график функции возникает и как самостоятельный способ задания функции. Приборы вычерчивают график зависимости одной величины от другой (чаще всего от времени).

в) Аналитический. Аналитическим способом, т. е. с помощью одной формулы можно задавать только элементарные функции. Это самый универсальный способ задания функции, из которого можно получить и таблицу и график.