 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Розв’язання. Дане рівняння - лінійне неоднорідне диференціальне рівняння 2-го порядку зі сталими коефіцієнтами
|
|
Дане рівняння - лінійне неоднорідне диференціальне рівняння 2-го порядку зі сталими коефіцієнтами. Запишемо відповідне лінійне однорідне рівняння 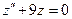 . Його характеристичне рівняння має вигляд:
. Його характеристичне рівняння має вигляд:
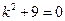 .
.
Його корені 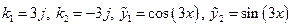 .
.
Тоді загальним розв'язком відповідного лінійного однорідного рівняння є
 .
.
Загальний розв'язок вихідного рівняння будемо шукати методом варіації сталих – методом Лагранжа, тобто у вигляді
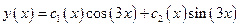 .
.
Функції 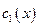 та
та 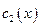 знайдемо із системи
знайдемо із системи
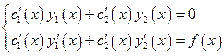
Маємо
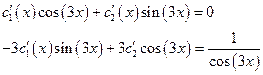
Розв’яжемо дану систему за формулами Крамера:
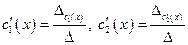 , де
, де
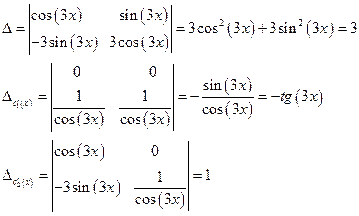
Тоді
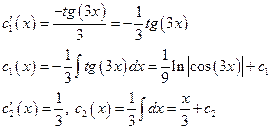
Загальний розв'язок вихідного рівняння буде мати вигляд

або 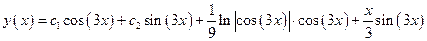 .
.
Завдання 16. Знайти загальний розв’язок системи диференціальних рівнянь: 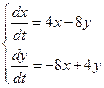
Дата публикования: 2014-10-20; Прочитано: 408 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
