 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Відповідь :
|
|
Завдання 13. Знайти загальний розв’язок рівняння:

Розв’язання. Дане рівняння - лінійне неоднорідне рівняння іншого порядку зі сталими коефіцієнтами та спеціальною функцією в правій частині.
Характеристичне рівняння

має корені 

 .
.
Тоді загальний розв'язок лінійного однорідного рівняння набуває вигляду
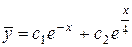 .
.
Для функції  при
при 


 [1, с.81] частинний розв'язок неоднорідного рівняння можна знайти у вигляді (5.89) [1, с.83].
[1, с.81] частинний розв'язок неоднорідного рівняння можна знайти у вигляді (5.89) [1, с.83].
Отже,  .
.
Для знаходження  підставимо
підставимо  у вихідні рівняння:
у вихідні рівняння:
 ,
,
або
 .
.
Прирівнюючи коефіцієнти при  , дістаємо
, дістаємо

Тоді загальний розв'язок лінійного неоднорідного рівняння приймає вигляд
 .
.
Відповідь:  .
.
Завдання 14. Розв’язати задачу Коші:
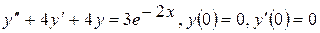 .
.
Дата публикования: 2014-10-20; Прочитано: 399 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
