|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Векторами в координатной форме
|
|
. 2.1. Декартов ортонормированный базис
Определение. Векторы  образуют правую тройку векторов, если из конца вектора
образуют правую тройку векторов, если из конца вектора  кратчайший поворот от вектора
кратчайший поворот от вектора  к вектору
к вектору 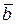 виден против часовой стрелки и левую тройку векторов, если кратчайший поворот виден против часовой стрелки.
виден против часовой стрелки и левую тройку векторов, если кратчайший поворот виден против часовой стрелки.

|
 
| Векторы  на рис.4 образуют левую тройку векторов,
на рис.5 на рис.4 образуют левую тройку векторов,
на рис.5 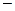 правую тройку. правую тройку.
|
Определение. Если в  задан базис
задан базис  и
и  , то базис
, то базис
называется ортогональным. Если  и,
и,  , то базис
, то базис
называется ортонормированным. Если  ,
,  и
и  образуют правую тройку векторов, то базис называется декартовым ортонормированным.
образуют правую тройку векторов, то базис называется декартовым ортонормированным.
Определение. Если в трехмерном пространстве заданы: 1) произвольная точка О 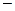 начало отсчета и 2) декартов ортонормированный базис
начало отсчета и 2) декартов ортонормированный базис  то говорят, что в пространстве задана декартова прямоугольная система координат.
то говорят, что в пространстве задана декартова прямоугольная система координат.
Прямые, проходящие через начало координат, называются осями координат: ОХ 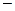 ось абсцисс; OY
ось абсцисс; OY 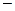 ось ординат; OZ
ось ординат; OZ 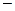 ось аппликат.
ось аппликат.
Векторы 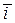 , , 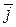 , , 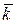 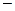 называются координатными ортами. называются координатными ортами.
 координатная прямая
координатная прямая
|  система координат
на плоскости
система координат
на плоскости
|  система координат
в пространстве
система координат
в пространстве
|
Дата публикования: 2014-10-20; Прочитано: 370 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!