 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные операции над геометрическими векторами
|
|
Линейными операциями над векторами называют операцию сложения векторов и операцию умножения вектора на скаляр (число).
| 1. Сложение векторов. | ||||
 а) Правило треугольника: а) Правило треугольника:  . Суммой векторов . Суммой векторов  и и  называется вектор называется вектор  , идущий из начала первого вектора в конец второго или , идущий из начала первого вектора в конец второго или  . .
| ||||
 б) Правило многоугольника б) Правило многоугольника  или или
  . .
| ||||
 в) Если векторы образуют замкнутый многоугольник, как показано на рисунке, то сумма векторов равна нулю: в) Если векторы образуют замкнутый многоугольник, как показано на рисунке, то сумма векторов равна нулю:

| ||||
г) Правило параллелограмма:  . Под суммой двух векторов . Под суммой двух векторов
| ||||

| с общим началом понимается вектор  , выходящий из общего начала и совпадающий по длине и направлению с диагональю параллелограмма, построенного на этих векторах. , выходящий из общего начала и совпадающий по длине и направлению с диагональю параллелограмма, построенного на этих векторах.
| |||
| 2. Вычитание векторов. | ||||

«уменьшаемого» (вторая диагональ параллелограмма), Выражение | ||||
| 3. Умножение вектора на число. | ||||

| При умножении вектора на число  длина вектора умножается на это число, а направление не изменяется. При умножении вектора на число длина вектора умножается на это число, а направление не изменяется. При умножении вектора на число  длина умножается на число длина умножается на число  , а направление изменяется на противоположное. , а направление изменяется на противоположное.
| |||
Дата публикования: 2014-10-20; Прочитано: 475 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

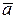 и
и  понимается вектор
понимается вектор  , который в сумме
вектором
, который в сумме
вектором 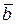 дает вектор
дает вектор  .
Другими словами, это вектор, идущий из
конца «вычитаемого» вектора в конец
.
Другими словами, это вектор, идущий из
конца «вычитаемого» вектора в конец
 .
. можно записать иначе
можно записать иначе  . Эту формулу читают так: чтобы из
. Эту формулу читают так: чтобы из