 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Векторы и Линейные операции над ними
|
|
Основные понятия
1. Величины бывают скалярными и векторными. Скалярные величины определяются своими численными значениями, например, масса, время, длина, площадь, объём и др. Такие величины как ускорение, сила, момент силы и др. имеют две характеристики численное значение и направление и называются векторными или векторами. Для обозначения вектора используют отрезок, на котором указано направление, т.е. направленный отрезок, его обозначают 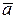 или
или 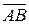 , где точка
, где точка 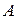 есть начало вектора
есть начало вектора 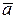 , точка
, точка 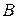
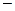 конец вектора
конец вектора 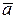 (рис.1). Начало вектора будем называть точкой приложения.
(рис.1). Начало вектора будем называть точкой приложения.
|
 Определение.Вектор, длина которого равна единице, называется единичным вектором или ортом направления. Обозначается Определение.Вектор, длина которого равна единице, называется единичным вектором или ортом направления. Обозначается  .
Вектор .
Вектор  имеет длину равную единице имеет длину равную единице  и сохраняет направление вектора
и сохраняет направление вектора 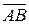 .
Орты на плоскости изображены на рис.2 .
Орты на плоскости изображены на рис.2
|
3. Определение. Два вектора называются равными, если они имеют
одинаковую длину и одинаковое направление. На рис.3 изображён ромб
 со стороной, равной 1. Тогда
со стороной, равной 1. Тогда  , но
, но  .
.
Рис. 3

| Векторы 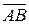 и и  называются противоположными. называются противоположными.  Сумма противоположных векторов равна нулю, т.е. Сумма противоположных векторов равна нулю, т.е.  .
Замечание: .
Замечание:  или или  . .
|
4. Определение. Два вектора или более, лежащие на параллельных
прямых или на одной прямой, называются коллинеарными. Обозначается  . На рис.3
. На рис.3  или
или  ,
,  ,
, 

 и т. д.
и т. д.
Определение. Так как направление нулевого вектора не определено, то он коллинеарен любому вектору.
Определение. Два вектора называются ортогональными, если они лежат на перпендикулярных прямых. Обозначается  .
.
Определение. Три или более векторов, лежащих в параллельных плоскостях (или в одной плоскости), называются компланарными. На рис.3 все векторы компланарны. Нулевой вектор компланарен любой системе компланарных векторов.
Дата публикования: 2014-10-20; Прочитано: 413 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!


 или
или  . Вектор, длина которого равна нулю,
называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю,
называется нулевым вектором и обозначается  или просто 0.
или просто 0.