Задания для самостоятельной работы. 1.Дан неориентированный граф (неограф) G = (V,R), где V = {1,2,3,4,5,6,7} – множество вершин неографа (вершины помечены натуральными числами)

1. Дан неориентированный граф (неограф) G = (V,R), где V = {1,2,3,4,5,6,7} – множество вершин неографа (вершины помечены натуральными числами), R = {(1,2),(2,3),(1,6),(2,4),(2,5),(3,4),(2,6)} – множество ребер неографа. Какой вид имеет матрица смежностей данного неориентированного графа?

2.

3. Чему равно число полных путей в ориентированном графе, представленном следующей матрицей смежности?

	A	B	C	D
A
B
C
D

4. Неориентированные графы имеют множество вершин {A,B,C,D}. Множества их ребер заданы отношением инцидентности: каждое ребро представлено как пара вершин. Поставьте в соответствие каждому графу его изображение.

1) {(A,C),(B,C),(C,D),(B,D)};

2) {(A,B),(A,C),(B,C),(C,D)};

3) {(A,C),(B,C),(B,D),(B,B)};

а б в г д

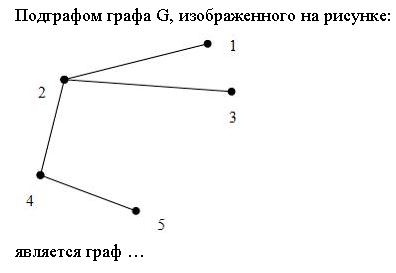
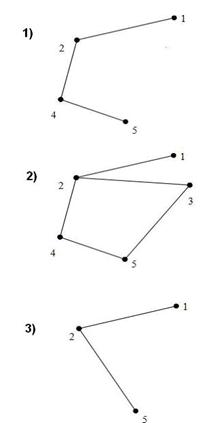
5. Какой маршрут является циклом на графе G, изображенном на рисунке:

1) 12543;

2) 12541;

3) 145341;

4) 1231.

6. Для ориентированного графа, изображенного на рисунке,

полный путь имеет вид:

a) L: 1→2→4

b) L: 0→1→2→3→4

c) L: 0→3→2→4

d) L: 0→4

7. Чему равна матрица смежности и инцидентности следующего ориентированного графа:

8. Чему равна матрица смежности и инцидентности следующего ориентированного графа:

9. Построить коды плоских корневых деревьев, изображенных ниже:

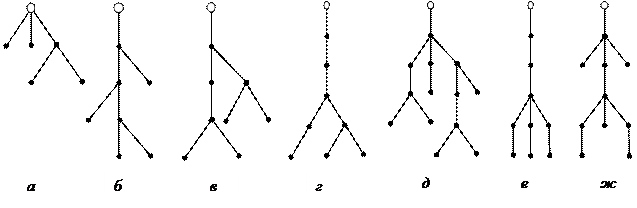
10. Построить плоское корневое дерево по его коду :

1) = 0010100111

2) = 00110101000111

3) = 0000010011011111

4) = 01001000110111

5) = 00100010110111;

6) = 00010111010000101111

11. По вектору установить, является ли он кодом какого-либо плоского дерева:

1) = 001011

2) = 0110

3) = 001001

4) = 010011

5) = 00111001

6) = 0001100111

12. Множество векторов A разбить на классы так, чтобы каждый класс состоял из кодов попарно изоморфных плоских корневых деревьев.

1) A = { ₁ = 0100101101, ₂ = 0101000111, ₃ = 0001110101,

₄ =0101001011, ₅ = 0100011101}.

2) A = { ₁ = 0100010110111, ₂ = 000110011101, ₃ = 001001011101,

₄ =010010010111, ₅ = 010001100111}

3) A = { ₁ = 0011010011, ₂ = 0100110011, ₃ = 0010110101,

₄ =0100101101, ₅ = 0011001101}.

ЛИТЕРАТУРА