Единственность представления булевых функций полиномами Жегалкина

Теорема 6. Каждая функция 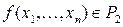может быть представлена в виде полинома Жегалкина, причем единственным образом.

Доказательство:

1) По следствию 3 теоремы 3

. (4)

Нам необходимо избавиться от отрицаний в сумме (4). Воспользуемся формулой , так как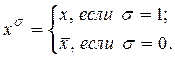

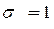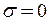Действительно: если , то , если , то .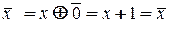

Преобразуем формулу (4):

.

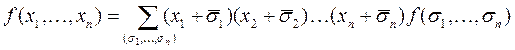В нашей сумме уже нет отрицаний над переменными. Теперь раскроем скобки: 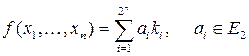, 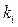– различные конъюнкции от переменных . Таким образом, мы показали, что каждая функция из представима в виде полинома Жегалкина.

2) Докажем единственность. Для этого подсчитаем число полиномов и сравним с числом функций от n переменных.

Выпишем все различные конъюнкции 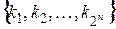, каждая коньюнция либо входит в полином, либо не входит, поэтому полиномов всего будет 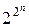. Число функций | |= .

Вывод:

1) Получили, что число полиномов равно числу функций от 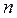переменных.

2) Каждая функция представляется хоть каким-нибудь полиномом.

3) Каждый полином реализует только одну функцию.

Таким образом, представление функции в виде полинома единственно.

Теорема полностью доказана.