Свойства математического ожидания и дисперсии

1) , где – постоянная.

2) .

3) .

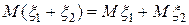4) .

Если , то .

Случайная величина 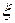называется неотрицательной , если она принимает только неотрицательные значения.

5) Если , то .

6) , где – постоянная.

7) .

8) .

Если , то .

9) . – постоянная.

10) .

11) .

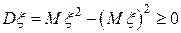
Двумерная случайная величина называется распределенной по нормальному закону, если ее плотность распределения

.

Здесь , , , ,

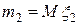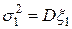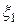– коэффициент корреляции случайных величин и 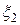. Для нормальной случайной величины понятия независимости и некоррелируемости эквивалентны.

Двумерная случайная величина распределена равномерно в области , если ее плотность распределения

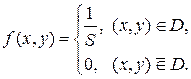
Здесь – площадь области .

Пример 1. Дискретная двумерная случайная величина распределена по закону, приведенному в таблице

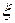
	–1
–1	0,2	0,1	0,3
	0,1	0,1	0,2

Определить:

1) Законы распределения составляющих и , , ;

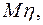
2) условный закон распределения случайной величины при условии, что ;

3) ;

4) коэффициент корреляции .

Решение. 1) Случайная величина может принимать два значения и .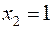

Событие, состоящее в том, что случайная величина примет значение , представляет собой сумму трех несовместных событий: 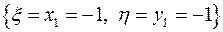, , . По теореме сложения вероятностей вероятность события, состоящего в том, случайная величина примет значение , будет равна сумме вероятностей этих событий. Практически для нахождения достаточно просуммировать вероятности первой строки двумерного закона распределения.

Аналогично находятся вероятности и других значений случайных величин и .

Законы распределения составляющих будут иметь вид

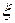
	–1
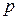
	0,6	0,4

	–1
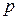
	0,3	0,2	0,5

,

,

,

.

2) Условный закон распределения случайной величины при условии, что – это перечень возможных значений случайной величины и условных вероятностей , которые вычисляются по формуле ,

,

.

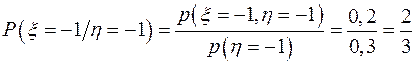Условный закон распределения случайной величины при условии, что будет иметь вид

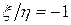
	–1

Сравнивая закон распределения случайной величины и условный закон распределения случайной величины , видим, что закон распределения случайной величины зависит от того, какое значение принимает случайная величина . Следовательно, – зависимые случайные величины.

3) Условное математическое ожидание дискретной случайной величины равно .

Для решаемой задачи .

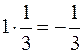4) Коэффициент корреляции .

Корреляционный момент 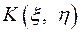для дискретной двумерной случайной величины равен .

Для решаемой задачи

.

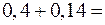
Вычислим коэффициент корреляции

.

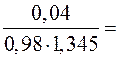
Пример 2. Пусть задан треугольник АВС с вершинами А(0,0), В(1,0), С(0,1). Обозначим область, ограниченную треугольником АВС через D. Двумерная случайная величина имеет равномерное распределение вероятностей в треугольной области , то есть

Найти постоянную , одномерные плотности , случайных величин и , коэффициент корреляции , условную плотность и условное математическое ожидание .

Рис. 3

Решение. 1) Постоянную найдем из условия нормировки

, ,

где – площадь треугольника . Значит

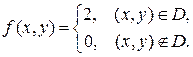
2) Уравнение прямой ВС имеет вид . Тогда область можно аналитически задать следующим образом:

или .

3)

.

.

.

.

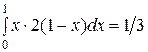4) .

.

5)

.

Пример 3. Пара случайных величин и имеет совместное нормальное распределение с вектором математических ожиданий и ковариационной матрицей :

.

Известно, что . Найти .

Решение. Совместная нормальность пары случайных величин и обеспечивает нормальность каждой из них и любой их линейной комбинации, в частности величина нормальна с параметрами

, .

Подставляя в последнее соотношение элементы ковариационной матрицы

, , ,

получим

.

По условию 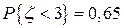, откуда, используя нормальность , получаем

.

Здесь функция распределения вероятности случайной величины , .

Искомые дисперсии равны, соответственно,

, .

Пример 4. Случайный вектор имеет вектор математических ожиданий и корреляционную матрицу .

, .

Вычислить вектор математических ожиданий случайного вектора и корреляционную матрицу вектора .

Решение. .

.

. .

.

=

.

Ответ: , .