Функция и ее свойства

Пусть – линейное пространство. Отображение , то есть правило, согласно которому всякому ставится в соответствие число, называется функционалом.

Функционал называется линейным, если для любых и любых чисел и

.

Всюду в дальнейшем в качестве линейного пространства будем понимать { , вблизи концов интервала}. То есть – это линейное пространство бесконечно дифференцируемых функций, определенных на интервале , тождественно равных нулю вблизи концов этого интервала. Действие функционала на функцию , 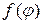будем записывать так:

.

Примеры линейных функционалов на

а) Всякая кусочно-непрерывная функция порождает линейный функционал на вида

.

б) .

Такой функционал, который любой функции ставит в соответствие значение этой функции в точке 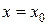, называется - функцией.

По аналогии с а) действие - функции записывают в виде интеграла

Последнее равенство называют фильтрующим свойством -функции.

Производной функционала назовем функционал , действующий по правилу , .

Так как , то любой функционал имеет бесконечное количество производных и .

Отметим следующие свойства 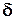- функции:

Если – функция Хевисайда, то .

.

Равенство справедливо для любой функции .

.

В частности, при , .