Свойства плотности распределения вероятности непрерывной случайной величины

1) .

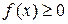2) .

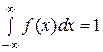3) 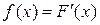в любой точке непрерывности .

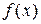4) .

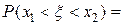
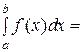
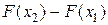Замечание. Для функции распределения 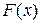дискретной случайной величины справедлива формула

,

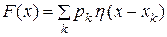где функция Хэвисайда. Дифференцируя последнее равенство, видим, что и для дискретной случайной величины можно ввести плотность распределения вероятности по формуле

.

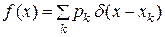Для случайных величин вводят понятия начальных и центральных моментов, из которых наиболее часто используются математическое ожидание и дисперсия.

Математическим ожиданием случайной величины 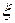называется число

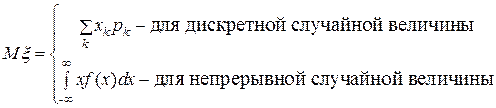(1)

Говорят, что математическое ожидание у случайной величины существует, если ряд (интеграл) (1) сходится абсолютно.

Дисперсией случайной величины 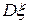называется число

.

Дисперсия вычисляется по формулам:

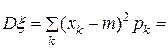
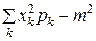для дискретной случайной величины.

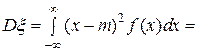
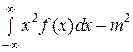для непрерывной случайной величины, где .

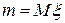Рассеивание возможных значений случайной величины от её математического ожидания часто характеризуют средним квадратическим отклонением .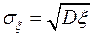

Существует достаточно большое число законов распределения дискретных и непрерывных величин, которые встречаются в приложениях. Параметры этих законов являются числовыми характеристиками случайных величин или же числовые характеристики выражаются через параметры законов распределения.