 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. Введем обозначение матриц
|
|
Введем обозначение матриц.
3 -2 1 А = 1 1 -2 4 -1 1 |   х1
Х = х2
х3
х1
Х = х2
х3
|   9
В = 0
13
9
В = 0
13
|
Тогда АХ = В - матричная запись системы уравнений.
Вычислим определитель матрицы А
| 3 -2 1 | ||||
| Δ = | А | = | 1 1 -2 | = 10 |
| 4 -1 1 |
| Δ = | А |
Т.к. = 10 ≠ 0, то матрица А невырожденная и имеет обратную А-1.
Х = А-1 В - решение системы уравнений в матричном виде.
Найдем обратную матрицу по формуле
 |  |
А11 А21 А31
А-1 = 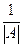 · (А*)Т =
· (А*)Т = 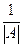 А12 А22 А32
А12 А22 А32
А13 А23 А33,
где | A| - определитель матрицы А.
А* - матрица, присоединенная для А.
(А*)Т - транспонированная матрица.
Аij - i, j = 1, 2, 3, алгебраические дополнения для элементов аij
в определителе | A|.
Вычислим алгебраические дополнения.
А11 = (-1)1+1  = -1. = -1.
| А21 = (-1)2+1 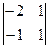 = 1. = 1.
| А31 = (-1)3+1 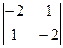 = 3. = 3.
|
А12 = (-1)1+2  =-9. =-9.
| А22 = (-1)2+2 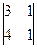 = -1. = -1.
| А32 = (-1)3+2 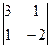 = 7. = 7.
|
А13 = (-1)1+3  = -5. = -5.
| А23 = (-1)2+3 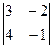 = -5. = -5.
| А33 = (-1)3+3 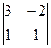 = 5. = 5.
|
Подставим их в формулу обратной матрицы
 |  |
-1 1 3
А-1 = 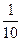 -9 -1 7
-9 -1 7
-5 -5 5
Найдем решение системы из матричного равенства
 |  |  |  |  |  |  |  |
х1 -1 1 3 9 -1 · 9 + 1· 0 + 3 · 13
х2 = 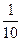 -9 -1 7 0 =
-9 -1 7 0 = 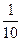 -9 · 9 - 1 · 0 + 7 · 13 =
-9 · 9 - 1 · 0 + 7 · 13 =
х3 -5 -5 5 13 -5 · 9 -5 · 0 +5 · 13
 |  |  |  |
30 3
= 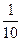 10 = 1
10 = 1
20 2
Ответ: х1 = 3, х2 = 1, х3 = 2.
| Задание II. | С помощью скалярного произведения векторов вычислить, какую работу производит сила
 =2 =2  -3 -3  ,
когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А (-4; 3) в положение В (2; 1) ,
когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А (-4; 3) в положение В (2; 1)
|
Дата публикования: 2014-10-20; Прочитано: 423 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

