Обратный ход метода Гаусса

Из третьего уравнения системы имеем х₃ = 3.

Подставляя значение переменной х₃ во второе уравнение, получим

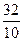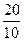х₂ = - + · 3 = - = -2

х₂ = -2.

Подставляя х₂ = -2 в первое уравнение, получим

х₁ = -8 - 3 (-2) +3=1.

Ответ: х₁ = 1, х₂ = -2, х₃ = 3.

в) Можно воспользоваться модификацией метода Гаусса. Совместив прямой и обратный ход метода Гаусса от расширенной матрицы системы перейдем к единичной матрице, что укорачивает процесс вычислений.

1 3 -1 -8

3 -1 1 8 <=>

2 1 -2 - 6

Шаг 1.

Из второй строки вычтем первую, умноженную на 3.

Из третьей строки вычтем первую, умноженную на 2.

1 3 -1 -8

3 - 1 · 3 -1 - 3 · 3 1 -(-1) · 3 8 - (-8) · 3 <=>

2 - 1 · 2 1 - 3 · 2 -2 -(-1)· 2 -6 - (-8) · 2

1 3 -1 -8

<=> 0 -10 4 32 <=>

0 -5 0 10

Шаг 2.

Разделим вторую строку на (-10), а третью на (-5).

<=> <=>

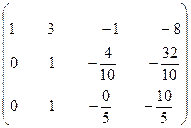Шаг 3.

Из первой строки вычтем вторую, умноженную на 3, а из третьей строки вычтем вторую.

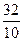1 - 0 3 - 1 · 3 -1 + · 3 - 8 + · 3

<=> 0 1 - - <=>

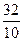0 1 - 1 - + - +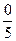

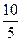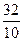
1 0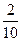

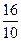
<=> 0 1 - - <=>

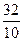0 0

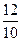
Шаг 4.

Разделим третью строку на .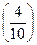

1 0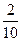

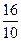
<=> 0 1 - -

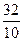
0 0 1 3

Шаг 5.

Вычтем из первой строки третью, умноженную на 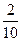, а из второй вычтем третью, умноженную на .

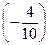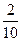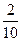
1 0 - - 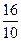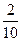·3 1 0 0 1

<=> 0 1 - + - 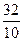+ 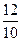<=> 0 1 0 -2

0 0 1 3 0 0 1 3

Получили матрицу, которая соответствует системе уравнений:

х1 = 1 х2 = -2 х3 = 3

Ответ: х₁ = 1, х₂ = -2, х₃ = 3.