 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
А) Метод Крамера
|
|
Вычислим определитель системы путем разложения по элементам третьей строки:
| ∆3= | 3 -2 1 1 1 -2 4 -1 1 | = 3 · (-1)1+1 | 1 -2 -1 1 | +(-2)·(-1)1+2 | 1 -2 4 1 | + 1 · (-1)1+3 | 1 1 4 -1 | = | ||
| = 3·(-1)+2·9+1·(-5)=10 | ||||||||||
∆ = 10.
Так как определитель системы ∆ = 10 ≠ 0, то система имеет единственное решение, которое находим по формулам Крамера
хi =  , i = 1, 2, 3. , i = 1, 2, 3.
|
где ∆ i - определитель, получаемый из определителя системы заменой i -
того столбца столбцом свободных членов.
| ∆1= | 9 -2 1 0 1 -2 13 -1 1 | = 9 · (-1)1+1 | 1 -2 -1 1 | +(-2)·(-1)1+2 | 0 -2 13 1 | + 1 · (-1)1+3 | 0 1 13 -1 | = | ||
| =9·(-1)+2·25+1·(-13)=30 | ||||||||||
∆1 = 30.
| ∆1= | 3 9 1 1 0 -2 4 13 1 | = 3 · (-1)1+1 | 0 -2 13 1 | +9·(-1)1+2 | 1 -2 4 1 | + 1 · (-1)1+3 | 1 0 4 13 | = | |||
| =3·26-9·9+1·13=10 | |||||||||||
∆2 = 10.
| ∆3= | 3 -2 9 1 1 0 4 -1 13 | = 3 · (-1)1+1 | 1 0 -1 13 | +(-2)·(-1)1+2 | 1 0 4 13 | + 9 · (-1)1+3 | 1 1 4 -1 | = |
| = 3·13+2·13+9·(-5)=20. |
∆3 =20.
х1 = 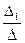 = =  = 3 = 3
| х2 =  = =  = 1 = 1
| х3 =  = = 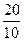 = 2. = 2.
|
Проверка.
Значения х1, х2, х3 подставим в данную систему уравнений
 | |||
 | |||
| 3 · 3 + (-2)·1 + 1·2 = 9 1 · 3 + 1 ·1 +(-2) ·2 = 0 4 · 3 + (-1)·1 +1·2 =13 | 9 = 9 0 = 0 13 = 13 |
Получили тождества, значит решение системы верно.
Ответ: х1 = 3, х2 = 1, х3 = 2.
Дата публикования: 2014-10-20; Прочитано: 325 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
