Простые и составные числа. Основная теорема арифметики

Определение. Натуральное число p называется простым, если p > 1 и p не имеет натуральных делителей, отличных от 1 и p.

Натуральное число n называется составным, если n > 1 и n имеет по крайней мере один натуральный делитель, отличный от 1 и p.

Число 1 не является ни простым, ни составным.

Замечание. В школьном курсе математики при определении простого и составного числа обычно «забывают» упомянуть, что - натуральные и большие единицы. При этом не упоминают и о натуральности делителей, так как в школе все делители натуральные.

Теорема 7.1. (Об основных свойствах простых чисел).

1)Любое натуральное число n>1 делится хотя бы на одно простое число.

2)Если простое число p делится на натуральное число n, то либо n=1, либо n=p.

3)Если произведение целых чисел делится на простое число p, то хотя бы один из сомножителей делится на p.

4)Если натуральное число n>1 является составным, то его наименьший простой делитель не превосходит числа .

5)Если натуральное число n не делится ни на одно простое число p , то n - простое.

Пример 3. Докажите, что число 127 простое.

Действительно, 127 – натуральное число, большее 1. Кроме того, 11< <12 и 127 не делится ни на одно простое число p, где p =2,3,5,7; 11< p <12. Значит, по свойству 5 теоремы 7.1, число 127 – простое.

Теорема 8.1. (Основная теорема арифметики). Всякое натуральное число n, большее единицы, либо просто, либо может быть представлено, причём единственным образом, в виде произведения простых чисел с точностью до порядка следования сомножителей.

Определение. Представление натурального числа n>1 в виде n = 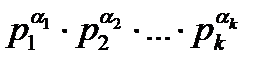, где - различные простые числа, -неотрицательное целое число, а - натуральные числа, называется каноническим разложением числа.

Следствие. Каждое натуральное число n>1 может быть представлено, причём единственным образом с точностью до порядка следования сомножителей, в каноническом виде.

Процесс представления числа n>1 в канонической форме называется факторизацией. Общий метод факторизации заданного числа заключается в том, что число n пробуют делить последовательно на простые числа 2, 3, 5,…, до тех пор, пока не найдётся простое число p такое, что n⋮p. Если такое p найдётся, то дальнейшая факторизация числа сводится к факторизации числа n₁ = , меньшего n. Если же среди всех указанных выше простых чисел нет ни одного делителя числа n, то, согласно свойству 5 теоремы 7.1, само число n простое, n=p₁ и n=p .

Пример 4. Представить в канонической форме (каноническом виде) натуральное число =5929.

Перебираем по порядку все простые числа 2, 3, 5 и т.д. и ищем среди них наименьший простой делитель числа 5929. По признакам делимости на 2, 3, 5 число 5929 на них не делится. А 5929=7∙847=7∙ n₁. Число n₁ не делится на 2, 3, 5, поэтому делим его вновь на 7: 847=7∙121=7∙ n ₂; n ₂ не делится на 2, 3, 5, 7. Поэтому делим n ₂ на следующее простое число p=11: 121=11∙11. Таким образом, n=7∙n₁=7∙7∙n₂=7∙7∙11∙11=7²∙11².

Теорема 9.1. (О распределении простых чисел в натуральном ряду).

1) (Теорема Евклида). Множество всех простых чисел бесконечно.

2) В натуральном ряду есть сколь угодно длинные интервалы, не содержащие простых чисел.

Теорема 10.1. (Решето Эратосфена).

1) Если во множестве натуральных чисел 2, 3, 4, 5, … n, зачеркнуть все числа, кратные первым r простым числам 2, 3, 5, …, p_r, то первое (наименьшее) не зачёркнутое число будет простым.

2) Если в этом множестве вычеркнуть все числа, кратные всем простым до (т.е. выбрать r так, чтобы p_r≤n<p_r+1), то оставшиеся не вычеркнутыми числа совпадают со множеством всех простых чисел p таких, что n≥p> .

Данная теорема даёт следующий алгоритм нахождения всех простых чисел в интервале от 2 до n: во множестве 2, 3, 4, 5, …, n - первое число 2 простое. Запоминаем 2 и вычёркиваем все числа, кратные 2. Тогда первое не вычеркнутое число 3 –простое. Запоминаем 3 и вычёркиваем из оставшихся все числа, кратные 3. Следующее первое не вычеркнутое число 5– простое и т.д. Продолжаем этот процесс до простого числа p_r включительно, где p_r≤ <p_r+1. Все оставшиеся не вычеркнутыми числа образуют множество всех простых чисел, лежащих между и n (включая и n, если оно простое, т.е. не вычеркнуто). А вместе с запомненными ранее простыми числами 2, 3, 5, …, p_r получится множество всех простых чисел, не превосходящих числа n.

Теорема 11.1. (Применение канонической формы).

1) Если n = - каноническая форма натурального числа n, то все натуральные делители числа n имеют вид c = , где 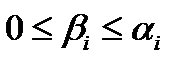, -целые числа для всех i=1, 2, …, k.

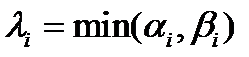2) Если a, b -натуральные числа, причём a = , b = , где p₁, p₂, …,p_k –различные простые числа, а ≥0, ≥0 -целые числа (согласованное представление натуральных чисел a и b), то (a, b)= , где для всех ; [ a, b ]= , где для всех .

Замечание. Данные формулы обосновывают известные школьные способы нахождения НОД и НОК натуральных чисел.

6. Числовые функции.

Числовые функции – это функции, заданные на множестве всех натуральных чисел N и связанные с арифметической природой натуральных чисел.

Определение.

–количество всех натуральных делителей натурального числа n.

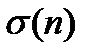-сумма всех натуральных делителей числа n, взятых ровно по одному разу.

-количество всех натуральных чисел, не превосходящих n и взаимно простых с числом n.

Функция 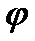называется функцией Эйлера.

Пример 5. Вычислить , , .

Так как 12⋮1, 2, 3, 4, 6, 12 – все натуральные делители числа 12. Поэтому , =1+2+3+4+6+12=28. Натуральные числа 1, 5, 7, 11 и только они не превосходят 12 и взаимно просты с 12. Значит, =4.

Теорема 12.1. Пусть 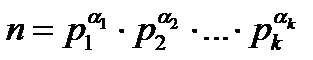- каноническое разложение числа натурального числа n>1. Тогда

Определение. Целой частью действительного числа α называется наибольшее целое число k такое, что . Дробной частью – разность между α и целой частью α.

Обозначения. – целая часть числа α; - дробная часть числа α. Итак, [α] – целое число и .

Пример 6.

Следствия. 1) Для любых натуральных чисел и 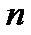количество натуральных чисел, кратных и не превосходящих , равно . 2) Показатель, с которым простое число входит в каноническое разложение числа , равен .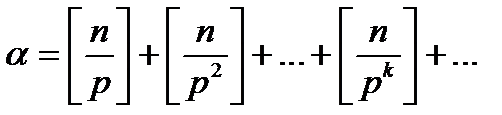

Замечание. Количество ненулевых слагаемых в данной формуле конечно.