 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ряд Дирихле
|
|
Ряд 
где p>0, называется рядом Дирихле. Этот ряд сходится при 
и расходится при 
. Частным случаем ряда Дирихле (при 
) является гармонический ряд 
.
Задание 3. Исследовать на сходимость по признакам сравнения:
1) 
| 6) 
|
2) 
| 7)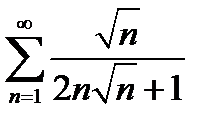 
|
3) 
| 8)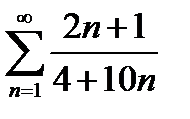 
|
4) 
| 9) 
|
5) 
| 10) 
|
Признак Даламбера. Если для ряда с положительными членами 
выполняется условие 
то ряд сходится при 
и расходится при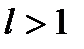 
.
Признак Даламбера не даёт решения, если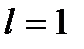 
. В этом случае для исследования ряда применяются другие признаки.
Задание 4. Исследовать на сходимость по признаку Даламбера:
1) 
| 6) 
|
2) 
| 7) 
|
3) 
| 8) 
|
4) 
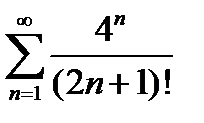
| 9) 
|
5) 
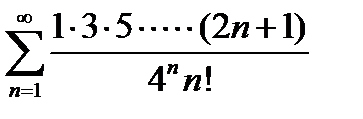
| 10) 
|
Интегральный признак Коши. Пусть функция f(x) при x ≥1 удовлетворяет условиям:
1) непрерывна,
2) положительна,
3) монотонно убывает.
Тогда числовой ряд 
, где 
= f(n), n ≥1 сходится или расходится
одновременно со сходимостью или расходимостью интеграла 
Задание 5. Исследовать на сходимость по интегральному признаку Коши следующие ряды:
1) 
2) 
3) 
4) 
5) 
| 6) 
7) 
8) 
9) 
10) 
|
Дата публикования: 2014-10-20; Прочитано: 1016 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
