Формула Тейлора

Рассмотрим важную задачу, которая решается в теории функциональных рядов: по заданной функции найти сходящийся функциональный ряд того или иного типа, сумма которого в области сходимости равнялась бы заданной функции. Такая задача называется разложением функции в ряд, например, степенной.

Пусть функция определена в некоторой окрестности точки

х ₀: , где , причём в этой окрестности функция имеет все производные до -го порядка.

Задача: Подберём многочлен n -й степени

по степеням так, чтобы в точке х ₀ совпадали значения и , а также значения их производных до ()-го порядка включительно. Тогда считаем, что в окрестности точки х ₀ такой многочлен будет приближать данную функцию с некоторой точностью.

Коэффициенты многочлена являются неопределенными коэффициентами, которые необходимо найти исходя из следующих условий:

, , , …, .

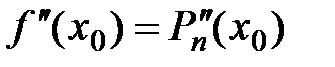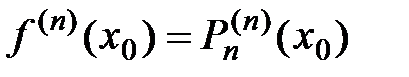Для нахождения этих коэффициентов найдём производные до n -го порядка от :

,

,

…

,

, при всех R.

Подставим в эти соотношения и приравняем , где :

, , ,

, … .

Находим выражения для , решая полученную систему уравнений:

.

Получаем общую формулу для определения коэффициентов многочлена :

, . (4)

Тогда многочлен примет следующий вид: .
Этот многочлен называется многочленом Тейлора для функции

по степеням , где называются коэффициентами многочлена Тейлора, .

Таким образом, для каждой функции , удовлетворяющей поставленным условиям при , можно найти многочлен Тейлора (в точке х ₀ функция и многочлен совпадают со своими производными до n -го порядка).

Разность , обозначенную через , называют остаточным членом формулы Тейлора, которая имеет вид:

(5)

Формула (5) называется формулой Тейлора для функции по степеням порядка n. Отметим, что

.

Величина остаточного члена формулы Тейлора играет важную роль в оценке точности приближения заданной функции многочленом Тейлора. Существует два вида остаточных членов.

1) Остаточный член в форме Пеано. Преобразуем остаточный член формулы Тейлора, используя некоторые понятия из теории пределов.

а) Функция 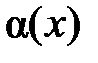называется бесконечно малой при , если .

б) Бесконечно малая функция называется бесконечно малой более высокого порядка малости относительно бесконечно малой функции 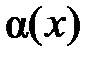при , если существует и записывается следующим образом: (что читается так: «β есть о малое от α).

Рассмотрим формулу Тейлора для функции по степеням
порядка n: . Остаточный член в формуле Тейлора имеет вид: . Из построения многочлена Тейлора следует Тогда откуда остаточный член формулы Тейлора можно записать в виде: , т.е. величина остаточного члена есть бесконечно малая более высокого порядка малости относительно при .

Формула Тейлора , в которой ,
называется формулой Тейлора с остаточным членов в форме Пеано. Поскольку остаточный член при является бесконечно малой величиной, то можно считать, что разность бесконечно мала, т.е. .

2) Остаточный член в форме Лагранжа. Запишем остаточный член в виде

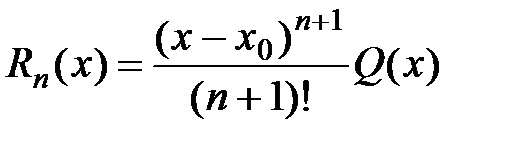, где Q (x) есть некоторая функция, подлежащая определению. Можно доказать, что , где точка ξ заключена между х и х ₀: , т.е. остаточный член имеет вид: . Тогда формула Тейлора примет вид , который называется формулой Тейлора с остаточным членом в форме Лагранжа.

Рассмотрим частные случаи формулы Тейлора.

– Если в формуле Тейлора с остаточным членом в форме Лагранжа положить , то получаем формулу конечного приращения: (теорема Лагранжа).

– Если в формуле Тейлора положить , то получим формулу, которую называют формулой Маклорена:

,

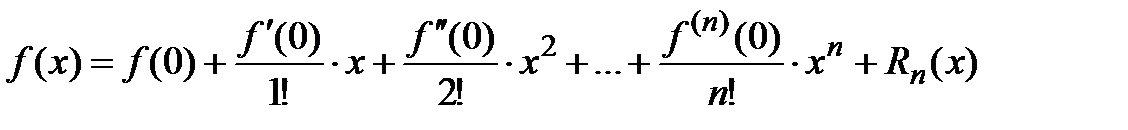где остаточный член можно записать в форме Пеано: или в форме Лагранжа:

.

Формула Маклорена является разложением функции в виде многочлена по степеням х.

Пример 5. Разложить функцию в виде многочлена третьего

порядка по степеням 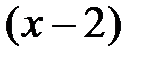с остаточным членом в форме Лагранжа.

Решение. Запишем формулу Тейлора для функции в точке в

виде многочлена 3-го порядка с остаточным членом в форме Лагранжа

,

где .

Находим производные нужного порядка в точке :

, ; , ;
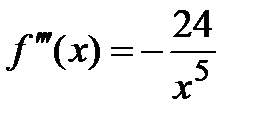, ; , ; , , где .

Полученные данные подставляем в формулу Тейлора и вычисляем .

Можно сказать, что функция заменяется многочленом с точностью, которую можно определить, оценив остаточный член формулы Тейлора при .