Числовые ряды

Ряды бывают: числовые, функциональные, степенные, конечные и бесконечные, знакопеременные.

Опр. Числовым рядом называется выражение вида , где числа.

Для сокращенного обозначения рядов используют знак

Пример.

Опр. Сумма первых n элементов ряда называется частичной суммой ряда .

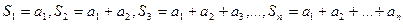
Опр. Ряд называется сходящимся, если последовательность его частичных сумм сходится, т.е. , где S – сумма ряда. (если предел не существует или равен , то ряд расходится).

Пример. Определить сходимость ряда - геометрическая прогрессия.

Докажем сходимость каждого ряда.

Эти ряды являются рядами бесконечной геометрической прогрессии со знаменателем <1, тогда . Так как сумма ряда конечное число, то ряд сходится.

Т. (Необходимый признак сходимости рядов).

Если ряд сходится, то его общий элемент стремится к нулю, т.е. .

Пример. ряд расходится.

Признак Даламбера сходимости рядов.

Пусть дан ряд Допустим, что , тогда

1) Если p<1, то ряд сходится.

2) Если p>1, то ряд расходится.

Пример. ряд сходится.

Задача. Написать первые пять элементов ряда по заданному общему элементу и проверить сходится ли ряд.