Пример решения типовой задачи. В таблице представлено распределение 200 драгоценных изделий по количеству примесей в них Х (%) и стоимости Y (тыс

В таблице представлено распределение 200 драгоценных изделий по количеству примесей в них Х ( %) и стоимости Y (тыс. руб):

Х \ У	3-9	9-15	15-21	21-27	27-33	Более 33	итого
20-30
30-40
40-50
50-60
60-70
70-80
80-90
Итого

Необходимо:

1. Вычислить условные средние и и построить эмпирические линии регрессии.

2. предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии и построить их графики на одном чертеже с эмпирическими линиями регрессии;

б) вычислить коэффициент корреляции на уровне значимости 0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;

Решение:

Найдем условные средние по формулам

и .

, - середины соответствующих интервалов.

Найдем середины интервалов и запишем в таблицу:

Х \ У							итого
Итого

2а). Для нахождения уравнений регрессии вычисляем необходимые суммы. Для удобства их вычислений составим расчетные таблицы.

				80,714	6778,8
				66,852	21675,6
				54,812	54261,9
				51,11	66238,56
				42,714	44847,6
				40,33	21778,2
∑				-

				25,895	17223,5
				28,909	57239,82
				20,571	79198,35
				17,823	39388,83
				9,75
∑				-

Тогда уравнение линейной регрессии у на х, будет иметь вид

,

или

Тогда уравнение линейной регрессии х на у, будет иметь вид

,

или

Ниже представлены графики полученных уравнений регрессии совместно с соответствующей эмпирической регрессией

2б). Находим коэффициент корреляции

Так как , то связь между рассматриваемыми признаками высокая, и так как , то связь обратная.

Проверим гипотезу о значимости коэффициента корреляции, то есть проверим гипотезу и

.

Воспользуемся t - критерием Стьюдента, найдем и :

.

Так как , , то

.

Таким образом, так как , то коэффициент корреляции значимо отличается от нуля. Связь тесная и обратная.

2в). Для нахождения корреляционных отношений найдем средние квадратические отклонения для условных средних и по формулам

,

.

Получим

;

.

Тогда ; .

Корреляционное отношение показывает, что признак зависит от влияния признака 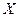, а отношение показывает, что признак 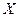зависит от влияния признака .

Контрольный тест после изучения раздела XIII «Элементы теории корреляции»

1. Регрессией Y на X называется:

а). Зависимость Y от X;

б). Теснота связи Y и X;

в). Изменение M (X/Y) при изменении Y;

г). Прямая, на которой лежат точки, соответствующие значениям системы;

д). Изменение M (Y/X) при изменении X.

2. Прямая регрессии Y на X имеет уравнение: . Какое из перечисленных значений может принимать коэффициент корреляции?

а). 5; б). 0,5; в). – 1; г). 1; д). - 0,5.

3. Корреляцией Y и X называется:

а). Зависимость Y от X;

б). Теснота связи Y и X;

в). Прямая, на которой лежат точки, соответствующие значениям системы;

г). Изменение M (Y/X) при изменении X, обладающее свойством монотонности;

4. Из того, что нет регрессии Y на X вытекает, что:

а). K =0;

б). Величины независимы;

в). Нет регрессии X на Y.

5. Прямая регрессии Y на X имеет уравнение: . Какое из перечисленных значений может принимать коэффициент корреляции?

а). 5; б). 0,5; в). – 1; г). 1; д). - 0,5.

6. Линейной корреляцией Y и X называется:

а). Тип зависимости Y от X;

б). Теснота связи Y и X;

в). Прямая, на которой лежат точки, соответствующие значениям системы;

г). Монотонная линейная зависимость условных математических ожиданий: M(Y/X) от Х, M (X/Y) от Y (одновременно).

7. Из того, что случайные величины Y и X независимы вытекает, что

а). K=0;

б). Плотность распределения системы равна нулю;

в). Нет регрессии X на Y;

8. Прямая регрессии Y на X имеет уравнение: . Какое из перечисленных значений может принимать коэффициент корреляции?

а). 5; б). 0,5; в). – 1; г). 1; д) - 0,5.

9. Если Y и X зависимы, то:

а). ;

б). Есть регрессия Y на X;

в). ;

10. Из того, что есть регрессия Y на X вытекает, что

а). ;

б). Величины зависимы;

в). Есть регрессия X на Y.

11. Линия регрессии Y на X имеет уравнение: . Величина Х принимает только положительные значения. Какое из перечисленных значений может принимать коэффициент корреляции?

а). 5; б). 0,5; в). – 1; г). 1; д) - 0,5.

12. Прямой регрессии Y на X называется:

а). Тип зависимости Y от; X

б). Прямая, на которой лежат точки, соответствующие значениям системы;

в). Наилучшая линейная аппроксимация зависимости M (Y/X) от Х.

13. Из того, что случайные величины Y и X связаны функционально вытекает, что

а) ;

б). Коэффициент корреляции по модулю равен единице;

в). Корреляционное отношение Y к X (или X к Y) равно единице;

14. Линия регрессии Y на X имеет уравнение: . Величина X >0. Какое из перечисленных значений может принимать коэффициент корреляции?

а). 5; б). 0,5; в). – 1; г). 1; д). - 0,5.