 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства корреляционных отношений
|
|
Корреляционное отношение удовлетворяет двойному неравенству
 и
и  .
.
Если  и
и  , то признаки
, то признаки 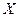 и
и  не связаны между собой корреляционной зависимостью.
не связаны между собой корреляционной зависимостью.
Если корреляционное отношение  , то между признаками
, то между признаками  и
и 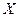 существует функциональная зависимость.
существует функциональная зависимость.
Выборочный коэффициент линейной корреляции  по абсолютной величине не больше корреляционных отношений, то есть
по абсолютной величине не больше корреляционных отношений, то есть
 и
и  .
.
Если  - это условные варианты признака
- это условные варианты признака 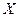 , и
, и  - это условные варианты признака
- это условные варианты признака  , то
, то
 и
и  .
.
Как показывает первое свойство, корреляционное отношение может принимать значения из промежутка от 0 до 1, причем, чем ближе значение корреляционного отношения к 1, тем теснее связь между рассматриваемыми признаками, и чем ближе это значение к 0, тем слабее связь между рассматриваемыми признаками.
Замечание: Как было сказано выше, корреляционное отношение служит мерой тесноты любой связи, в том числе и линейной формы. В этом состоит преимущество корреляционного отношения. Но так же оно имеет и недостатки: а) оно определяют только тесноту связи, но не указывают на направление связи, так как они вычисляются с помощью средних квадратических отклонений, которые всегда положительны; б) оно не позволяет судить на сколько близко расположены точки, найденные по данным наблюдений, к кривой определенного вида, например к параболе, гиперболе и т.д. Это объясняется тем, что при определении корреляционного отношения форма связи во внимание не принимается.
Пример. Распределение признаков 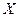 и
и  приведено в следующей корреляционной таблице
приведено в следующей корреляционной таблице
| X Y | ny | |||||||||
| -2 | ||||||||||
| -1 | ||||||||||
| nx |
Найти корреляционные отношения  и
и  , и сравнить их с соответствующим коэффициентом линейной корреляции.
, и сравнить их с соответствующим коэффициентом линейной корреляции.
Решение.
Найдем групповые средние:
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
 ;
;
 ;
;
 ;
;
 .
.
Для вычисления общих средних построим расчетные таблицы.

| 
| 
| 
| 
| 
|
| 1,75 | |||||
| 0,714 | |||||
| -0,2 | -20 | ||||
| -1,25 | -150 | ||||
| -2 | -160 | ||||
| -1,25 | -250 | ||||
| -0,2 | -60 | ||||
| 0,714 | |||||
| 1,75 | |||||
| ∑ | - |

| 
| 
| 
| 
| 
|
| -2 | -8 | -320 | |||
| -1 | -8 | -320 | |||
| ∑ | - |
Тогда:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 , следовательно, линейной связи между признаками
, следовательно, линейной связи между признаками 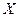 и
и  нет.
нет.
Для нахождения корреляционных отношений найдем средние квадратические отклонения для условных средних  и
и  по формулам
по формулам
 ,
,  .
.
Получим
 ;
;
 .
.
Тогда  ;
;  .
.
Корреляционное отношение  показывает, что признак
показывает, что признак  зависит от влияния признака
зависит от влияния признака 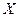 , а отношение
, а отношение  показывает, что признак
показывает, что признак 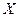 не зависит от влияния признака
не зависит от влияния признака  .
.
Дата публикования: 2014-10-20; Прочитано: 1616 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
