 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Оценка тесноты любой связи
|
|
Как рассматривалось выше, оценка тесноты линейной связи осуществляется с помощью выборочного коэффициента корреляции. Но связь между признаками 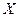 и
и  не всегда является линейной. Рассмотрим, как оценить тесноту любой корреляционной связи, как линейной, так и нелинейной.
не всегда является линейной. Рассмотрим, как оценить тесноту любой корреляционной связи, как линейной, так и нелинейной.
Пусть данные наблюдений над количественными признаками 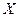 и
и  сведены в корреляционной таблице. Эти данные можно разбить на группы, причем каждая группа будет содержать те значения
сведены в корреляционной таблице. Эти данные можно разбить на группы, причем каждая группа будет содержать те значения  , которые соответствуют определенному значению
, которые соответствуют определенному значению 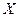 .
.
Пример. Пусть дана следующая корреляционная таблица
| x y | ny | |||
| nx |
Данные этой таблиц можно разбить на группы относительно признаков 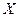 и
и  . Рассмотрим группы по признаку
. Рассмотрим группы по признаку  .
.
К первой группе относится 20 значений 
 , которые соответствуют
, которые соответствуют  .
.
Ко второй группе относится 31 значений 
 , которые соответствуют
, которые соответствуют  .
.
К третей группе относится 49 значений 
 , которые соответствуют
, которые соответствуют  .
.
Таким образом, в данном случае, все исходные значения по признаку  , можно разбить на три группы и вычислить групповые средние, которые совпадают с условными средними:
, можно разбить на три группы и вычислить групповые средние, которые совпадают с условными средними:
 ;
;  ;
;  .
.
Аналогично, можно разбить данные по признаку 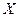 так же на три группы и найти групповые средние
так же на три группы и найти групповые средние  , получим
, получим
 ;
;  ;
;  .
.
После разбиения данных на группы и вычисления групповых средних можно вычислить средние квадратические отклонения условных средних  и
и  по формулам
по формулам
 ,
,
 .
.
С помощью этих средних квадратических отклонений, вычисляют корреляционные отношения  по
по 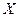 и
и 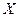 по
по  , по формулам
, по формулам
 и
и  ,
,
где  - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака 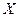 ;
;
 - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака  .
.
По приведенным корреляционным отношениям определяют тесноту любой связи, как линейной, так и нелинейной.
Дата публикования: 2014-10-20; Прочитано: 693 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
