 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример решения типовой задачи
|
|
Комитетом по физической культуре и спорту были проведены исследования спортсменов, занимающихся стрельбой. Было отобрано 200 стрелков из 4000 для определения среднего количества патронов, необходимых одному спортсмену для одной тренировки. Результаты обследования приведены в таблице
| Число патронов (шт.) | Менее 200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 | Более |
| Число спортсменов (чел.) |
1. Перейти к вариационному ряду, и построить полигон частот.
2. Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.
3. Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95.
4. Используя критерий 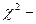 Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X– распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.
Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X– распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.
Решение.
1. Перейдем от данного интервального ряда к вариационному. Для этого найдем середину каждого интервала (сложим концы каждого интервала и поделим пополам):
| Число патронов (шт.), хi | |||||||
| Число спортсменов (чел.), ni |
Построим полигон частот для полученного вариационного ряда.
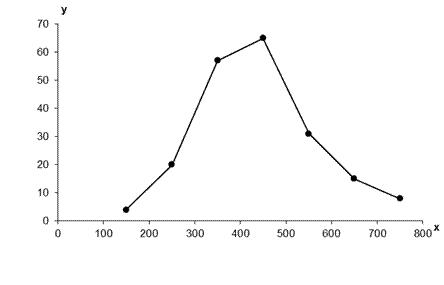
2. Находим выборочную среднюю по формуле:
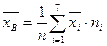 .
.
Объем выборки n =200.
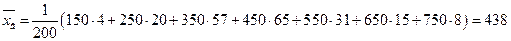
Таким образом, среднее число патронов необходимых одному спортсмену для одной тренировки равно 438 шт.
Находим выборочную дисперсию:
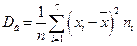 = 16656
= 16656
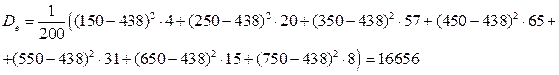
Посчитаем выборочную дисперсию вторым способом:
 , где
, где 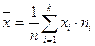 и
и 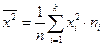 .
.
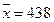

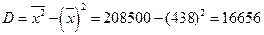
Среднеквадратическое отклонение: 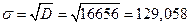
Исправленную выборочную дисперсию посчитаем по формуле:

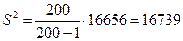
Исправленное выборочное среднеквадратическое отклонение случайной величины Х:
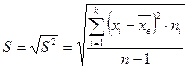
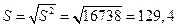
3. Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95. Тем самым, найдем границы, в которых с вероятностью 0,95 заключено среднее число патронов, необходимых для тренировки одного спортсмена.
Доверительный интервал для генеральной средней находим по формуле:
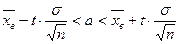 , где
, где  - математическое ожидание;
- математическое ожидание;
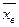 - выборочная средняя;
- выборочная средняя;
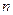 - объем выборки;
- объем выборки;
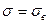 - при большом объеме выборки;
- при большом объеме выборки;
t - значение аргумента функции Лапласа, при котором она равна  , то есть
, то есть 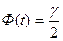 , где
, где 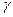 - заданная надежность. Аргумент t находится по таблицам значений функции Лапласа (приложение 2). По таблицам значений функции Лапласа находим: Ф(t)=0,95
- заданная надежность. Аргумент t находится по таблицам значений функции Лапласа (приложение 2). По таблицам значений функции Лапласа находим: Ф(t)=0,95  .
.
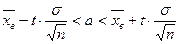
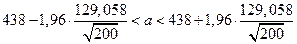 ;
; 
Доверительный интервал для оценки среднеквадратического отклонения  вычисляется по формуле
вычисляется по формуле
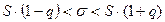 ,
,
где  - это исправленное среднеквадратическое отклонение;
- это исправленное среднеквадратическое отклонение;
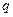 - это табличное значение, которое зависит от объема выборки
- это табличное значение, которое зависит от объема выборки 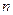 и заданной надежности
и заданной надежности 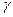 , то есть
, то есть 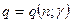 (приложение 4).
(приложение 4).
Найдем значение q: 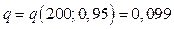
Тогда доверительный интервал для оценки среднеквадратического отклонения  будет равен:
будет равен:
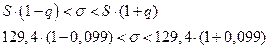
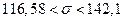
4. Используя критерий 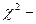 Пирсона при уровне значимости a=0,05 проверим гипотезу о том, что случайная величина X– распределена по нормальному закону.
Пирсона при уровне значимости a=0,05 проверим гипотезу о том, что случайная величина X– распределена по нормальному закону.
Примечание: В качестве дисперсии нормального закона распределения следует взять исправленную выборочную дисперсию. Но т.к. количество наблюдений – 200 достаточно велико, то подойдет и “обычная” 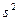 .
.
| x i | ni | 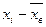
| 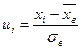
| 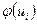
| 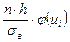
| 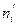
|
| -288 | -2,23 | 0,0332 | 5,144974 | 5,1 | ||
| -188 | -1,46 | 0,1374 | 21,29275 | 21,3 | ||
| -88 | -0,68 | 0,3166 | 49,06321 | 49,1 | ||
| 0,09 | 0,3973 | 61,56922 | 61,6 | |||
| 0,87 | 0,2732 | 42,33755 | 42,3 | |||
| 1,64 | 0,1040 | 16,11678 | 16,1 | |||
| 2,42 | 0,0213 | 3,300841 | 3,3 | |||
| 198,8 |
Составим расчетную таблицу для вычисления теоретических частот пользуюсь указанной схемой.
Для этого найдем величину 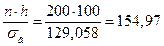 .(h -длина интервала или шаг).
.(h -длина интервала или шаг).
Из первого пункта данной задачи известно, что  .
.
Составим таблицу для подсчета 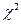
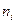
| 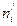
| 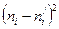
| 
|
| 5,1 | 1,21 | 0,237255 | |
| 21,3 | 1,69 | 0,079343 | |
| 49,1 | 62,41 | 1,271079 | |
| 61,6 | 11,56 | 0,187662 | |
| 42,3 | 127,69 | 3,018676 | |
| 16,1 | 1,21 | 0,075155 | |
| 3,3 | 22,09 | 6,693939 | |
| 198,8 | 11,56311 |
Итого, значение статистики 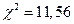 .
.
Определим количество степеней свободы по формуле:  .
.
m –число интервалов (m =7), r – число параметров закона распределения (в нормальном распределении r = 2)
Т.е. k = 7-2-1=4.
Соответствующее критическое значение статистики 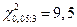
Поскольку 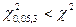 , гипотеза о нормальном распределении с параметрами N(438; 129,058) не согласуется с опытными данными.
, гипотеза о нормальном распределении с параметрами N(438; 129,058) не согласуется с опытными данными.
Ниже показана кривая эмпирического (сплошная линия) и теоретического (пунктирная линия) распределений

Вывод. Сопоставив обе кривых видим, что наилучшее соответствие эмпирических данных нормальному распределению наблюдается на первом, втором, и шестом интервалах, что подтверждается таблицей. А вот на участке от 500 до 600 патронов отклонение очень большое – это видно из графика. Оно и оказало “фатальное” влияние на критерий согласия – это видно из таблицы.
Контрольный тест после изучения разделов XI, XII «Статистическая проверка статистических гипотез»
1. Выборочное среднее равно 19,9. Гипотеза H0 для математического ожидания М
1).  ; 2).
; 2). 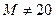 ; 3).
; 3). 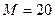 ; 4).
; 4). 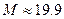 ; 5).
; 5). 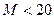 .
.
2. Относительная частота равна 0,25. Интервальная оценка вероятности может иметь вид:
1). (0; 1); 2). (0; 0,5); 3). (0,25; 0,5).
3. Статистическим аналогом математического ожидания является:
1). Абсолютная частота события;
2). Относительная частота события;
3). Выборочное среднее значение случайной величины.
4. Выборочное среднее равно 19. Интервальная оценка для математического ожидания М может иметь вид
1). (18; 20); 2). (17, 22); 3). (18; 21).
5. Совокупность наблюдений, отобранных случайным образом из генеральной совокупности, называется
| 1). | Репрезентативной | 2). | Вариантой |
| 3). | Выборкой | 4). | Частотой |
6. Объем выборки 1, 2, 2, 2, 3, 3, 4, 4, 6 равен …
7. Математическое ожидание оценки 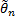 параметра
параметра 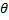 равно оцениваемому параметру. Оценка
равно оцениваемому параметру. Оценка 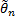 является
является
| 1) | Смещенной | 2) | Состоятельной |
| 3) | Несмещенной | 4) | Эффективной |
8. Оценка 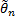 параметра
параметра 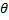 сходится по вероятности к оцениваемому параметру. Оценка
сходится по вероятности к оцениваемому параметру. Оценка 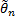 является
является
| 1) | Смещенной | 2) | Состоятельной |
| 3) | Несмещенной | 4) | Эффективной |
9. Произведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 8, 8. Тогда несмещенная оценка математического ожидания равна …
| 1) | 2) | 3) | 5,5 | 4) | 5,25 |
10. Выборочная дисперсия вариационного ряда равна 3,5. Объем выборки равен 50. Исправленная выборочная дисперсия равна …
| 1) | 3,43 | 2) | 3,57 | 3) | 0,07 | 4) | 3,5 |
11. Дана выборка объема n. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее 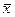 …
…
| 1) | Не изменится | 2) | Увеличится в 25 раз |
| 3) | Уменьшится в 5 раз | 4) | Увеличится в 5 раз |
12. Дан вариационный ряд
| варианта | |||
| частота |
Величина 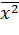 равна …
равна …
13. Дан вариационный ряд
| варианта | |||
| частота |
Выборочная дисперсия равна …
| 1) | 2) | 1,8 | 3) | 0,84 | 4) | 0,76 |
14. Дан вариационный ряд
| варианта | |||
| частота |
Исправленная выборочная дисперсия равна …
| 1) | 2) | 1,8 | 3) | 0,84 | 4) | 0,76 |
15. Относительная частота равна 0,25. Гипотеза H0 для вероятности P
16. 1). 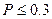 2).
2). 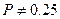 ; 3).
; 3).  ; 4).
; 4). 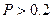 ; 5).
; 5). 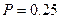 .
.
17. Множеством значений системы двух случайных величин является:
а) промежуток на числовой оси
б) часть координатной плоскости
в) числовая последовательность
18. Статистическим аналогом закона распределения системы двух дискретных случайных величин является
1). Гистограмма;
2). Дисперсия;
3). Корреляционная таблица;
4). Функция распределения вероятности.
19. Какие параметры имеет плотность равномерного закона?
1). Дисперсия; 2). Математическое ожидание;
3). Границы множества значений; 4). Интенсивность потока событий.
20. Дан интервальный вариационный ряд
| варианта | 1-3 | 3-5 | 5-7 | 7-9 |
| частота |
Выборочная средняя равна…
21. Статистическим аналогом вероятности события является
1). Абсолютная частота события;
2). Относительная частота события;
3). выборочное среднее значение индикатора события.
22. Сумма всех относительных частот дискретного вариационного ряда равна:
1). Значению функции распределения в точке х =1;
2). Вероятности достоверного события;
3). выборочному среднему значению случайной величины.
Дата публикования: 2014-10-20; Прочитано: 17570 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
