Методика вычисления теоретических частот нормального распределения

Пусть эмпирическое распределение задано в виде последовательности интервалов одинаковой длины и соответствующих им частот.

1. Находим выборочную среднюю, дисперсию, среднеквадратическое отклонение. В качестве вариант принимают среднее арифметическое концов интервала.

2. Нормируют случайную величину 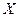, то есть переходят к величине и находят значения .

3. Находят значение функции Лапласа .

4.Вычисляют значение и умножают на .

5. Получаем теоретические частоты .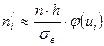

6. Сравниваем эмпирические и теоретические частоты. Для этого:

а) находим наблюдаемое значение критерия Пирсона:

.

Эта величина случайная, так как в различных опытах она принимает различные заранее не известные значения. Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина , то есть он характеризует близость эмпирического и теоретического распределения.

б) по таблице критических точек распределения 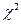, по заданному уровню значимости и числу степеней свободы , где 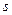- число групп выборки; - это число параметров предполагаемого распределения, которые оценены по данным выборки. найдем критическую точку .

Если - нет оснований отвергать нулевую гипотезу.

Если - нулевую гипотезу отвергают.

Замечание. В частности, если предполагаемое распределение – нормальное , то оценивают два параметра, математическое ожидание и среднее квадратическое отклонение, поэтому и число степеней свободы .

Пример: Дано следующее статистическое распределение выборки

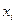
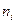
Найти теоретические частоты данного распределения и проверить гипотезу о нормальном законе этого распределения при уровне значимости с помощью критерия согласия 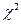Пирсона.

Решение:

Подсчитаем выборочную среднюю и среднеквадратическое отклонение.

и .

Составим расчетную таблицу для вычисления теоретических частот пользуюсь указанной схемой. Для этого найдем величину .(h -длина интервала или шаг).

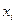
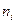
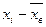
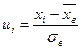
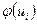
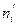
		-10	-1,73	0,0893	6,18
		-6	-1,04	0,2323	16,08
		-2	-0,35	0,3752	25,96
			0,35	0,3752	25,96
			1,04	0,2323	16,08	16,1
			1,73	0,0893	6,18	6,2
				0,054	3,73	3,7

Посчитаем величину

.

Воспользуемся расчетной таблицей

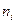
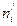
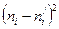
				2,67
		-2		0,25
				0,15
	16,1	-4,1	16,81	1,04
	6,2	1,8	3,24	0,52
	3,7	1,7	2,89	0,78
				5,41

Таким образом, .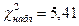

Найдем . Так как и , то .

Так как , то нет оснований отвергать гипотезу о нормальном законе распределения данной величины, то есть она принимается при уровне значимости и есть основания считать, что эмпирические и теоретические частоты различаются не значимо, различия случайны.