Біртексіз сызықты теңдеулер

5.1. Төмендегідей біртексіз сызықты теңдеуді қарастырайық:

(1)

Мұнда да коэффициенттер мен бос мүше кейбір 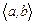аралығында үздіксіз функциялар деп есептелінеді. Осы теңдеудің сәйкес біртектісін қоса қарастырайық:

(2)

Бұл екі теңдеудің шешімдерінің арасында тығыз байланыстар бар.

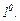Егер 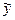біртексіз (1) теңдеудің шешімі, ал 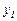біртекті (2)

теңдеудің шешімі болса, онда функциясы (1) теңдеудің шешімін береді.

Шынында да, . Осыдан

.

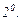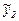Егер және функциялары (1) теңдеудің шешімдері болса, онда олардың айырмасы (2) теңдеудің шешімін береді.

Шыныда да, . Осыдан

.

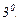Егер (1) теңдеуде болса, ал функциясы теңдеуінің шешімі болса, онда

Бұл қасиетті суперпозиция қасиеті деп атайды.

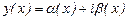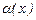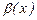Егер (1) теңдеудің оң жағы комплексты функция болса , ал комплексты функция сол теңдеудің шешімі болса, онда нақты және функциялары сәйкес және теңдеулерінің шешімдері болады.

Шынында да, . Осыдан тепе-теңдіктері шығады.

Осы қасиеттерді пайдалансақ, төмендегідей қорытындыға келеміз.

Теорема. Біртексіз (1) теңдеудің жалпы шешімі осы теңдеудің бір дербес шешімі мен сәйкес біртекті (2) теңдеудің жалпы шешімінің қосындысынан тұрады.

Дәлелдеуі. Айталық, 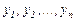біртекті (2) теңдеудің фундаменталь шешімдер жүйесі болсын, ал 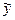функциясы біртексіз (1) теңдеудің бір дербес шешімі болсын. Бұл жағдайда

(3)

қосындысы берілген аралықта (1) теңдеудің жалпы шешім болатынын көрсетейік. Мұнда - еркін тұрақтылар. - қасиет бойынша (3) қосынды (1) теңдеудің шешімі:

Енді осы шешімнен кез келген Коши есебінің жалғыз ғана шешімін алуға болатынын көрсетсек, жеткілікті. Бастапқы шартты

(4)

түрінде алсақ, онда төмендегідей жүйе аламыз:

(5)

Бұл жүйе 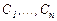сандары бойынша сызықты біртексіз алгебралық жүйе. Оның анықтауышы . Сондықтан, жүйенің нөлдік емес жалғыз ғана шешімі бар: . Осы сандарды (3) қатынасқа қойсақ, (1) теңдеудің (4) шартты қанағаттандыратын жалғыз ғана шешім аламыз.

5.2. Біртексіз теңдеудің жалпы шешімін табу үшін әдетте, тұрақтыларды вариациялау әдісі қолданылады. Бұл әдістің мәнісі – сәйкес біртекті теңдеудің жалпы шешімі белгілі деп, ондағы еркін тұрақтыларды 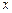-қа байланысты айнымалы шамалар деп есептелініп, шешім мына түрде ізделінеді:

(6)

мұндағы, 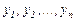- біртекті теңдеудің фундаменталь шешімдері. Осындағы функцияларын (6) қосынды (1) теңдеудің шешімі болатындай етіп таңдайды. Бұл функцияларды анықтау үшін теңдеу керек. Ол үшін (6) өрнекті ретке дейін дифференциалдаймыз. Мұнда функцияларының туындыларына қосымша шарт қойылып отырады.

Сонымен,

Осындағы екінші қосындыны нөлге теңейміз:

Қалған бірінші қосындыдан екінші туынды табамыз:

Осындағы екінші қосындыны тағы да нөлге теңейміз:

Осылай қосындыны 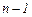рет дифференциалдап, туындыларының қосындысын әрдайым нөлге теңеп отырамыз. Сонда

,

ал

Соңғы екінші қосындыны нөлге теңестірмейді. Ол қосынды (1) теңдеудің оң жағындағы 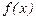функциясына тең деп алынады.

Себебі, (6) өрнекті және оның туындыларын (1) теңдеуге апарып қойсақ, төмендегідей теңдік аламыз:

мұнда . Сонымен, функцияларын анықтау үшін мынандай жүйе аламыз:

(7)

Бұл функциялары бойынша сызықты біртексіз алгебралық жүйе. Оның анықтауышы Вронский анықтауышы, ал ол нөлге тең емес. Өйткені, 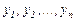шешімдері өзара сызықты тәуелсіз. Осы жүйені Крамер ережесі бойынша шешсек,

(8)

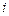өрнегін аламыз. Мұндағы, - Вронский анықтауышының -ші жатық жолы мен -нші тік жолының қиылысында тұрған элементтің алгебралық толықтауышы.

Соңғы қатынасты интегралдап, функциясын табамыз:

(9)

Мұндағы, -еркін тұрақтылар. Табылған осы функцияларды (6) қатынасқа қойсақ,

функциясын аламыз. Бұл функция өзінің құрылымы бойынша (1) теңдеудің шешімі. Мұндағы, бірінші қосынды (1) теңдеудің дербес шешімін, екінші қосынды біртекті теңдеудің жалпы шешімін білдіреді. Сонымен, бастапқы айтылған қағидаға қайта келдік: біртексіз теңдеудің жалпы шешімі осы теңдеудің бір дербес шешімі мен оның сәйкес біртектісінің жалпы шешімінің қосындысынан тұрады.