Шынында да, егер D облысында

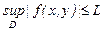
теңсіздігі орын алса, онда өсімше туралы Лагранж теоремасын пайдаланамыз:

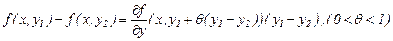Осыдан,

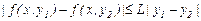
яғни, Липшиц шартын алдық. Ал Липшиц шартынан функцияның дифференциалдануы шыға бермейді. Оған бір мысал, 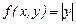функциясы. Бұл функция Липшиц шартын кез келген аралықта қанағаттандырады:

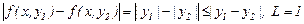
Алайда, бұл функцияның 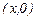нүктесінде у бойынша дербес туындысы анықталмаған.

Жалпы, Липшиц шарты функцияның бір аргументі бойынша бірқалыпты өсуін көрсетеді.

Ескерту-3. Тіктөртбұрыштың орнына кез келген шектелген тұйық облыс алуға болады. Бұл жағдайда 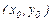нүктесі облыстың ішкі нүктесі болуы керек.

Ескерту-4. Теореманы 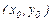нүктесін ішінде ұстайтын ашық облыста да дәлелдеуге болады. Ол үшін 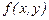функциясының осы облыста үздіксіз болуымен қатар, сол облыстың кез келген ішкі шектелген тұйық бөлігінде Липшиц шартын қанағаттандыруы тиіс.

Ескерту-5. Теоремадағы 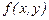функциясы тек үздіксіз ғана болса, яғни Липшиц шарты орындалмаса, онда теңдеудің бастапқы шартты қанағаттандыратын шешімі болады, бірақ ол жалғыз болмауы мүмкін. Бұл тұжырымды Пеано теоремасы айқындайды.