Негізгі түсініктер және анықтамалар. 1.1. Жоғарғы ретті жәй дифференциалдық теңдеудің туынды бойынша шешілмеген түрі былай жазылады:

1.1. Жоғарғы ретті жәй дифференциалдық теңдеудің туынды бойынша шешілмеген түрі былай жазылады:

(1)

Мұндағы, 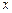-тәуелсіз айнымалы, 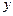-белгісіз функция, ал - белгісіз функцияның туындылары . - кейбір облысында анықталған нақты үздіксіз функция.

Егер (1) қатынас жоғарғы туындысы бойынша шешілсе, онда былай жазамыз:

(2)

Мұндағы, 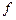- функциясы кейбір облысында анықталған үздіксіз функция деп есептелінеді.

Бұл теңдеулердің шешімдері де бірінші ретті теңдеулердің шешімдеріне ұқсас түрде анықталады.

Анықтама-1. аралығында анықталған функциясы (2) теңдеудің осы аралықтағы шешімі деп аталынады, егер ол төмендегідей үш шартты қанағаттандырса:

4) функциясы аралығында рет

дифференциалданатын болса;

5) ;

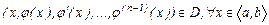6) .

Айқындалмаған (1) теңдеудің де шешімін осы түрде анықтауға болады.

Анықтама-2. аралығында анықталған функциясы (1) теңдеудің осы аралықтағы шешімі деп аталынады, егер ол төмендегідей үш шартты қанағаттандырса:

1) функциясы аралығында рет

дифференциалданатын болса;

2) ;

3) .

Жоғарғы ретті теңдеу үшін Коши есебі былайша қойылады: (2) теңдеудің барлық шешімдерінің ішінен

(3)

шартын қанағаттандыратын шешімді табу керек. Мұндағы, сандарын бастапқы мәндер, ал (3) шартты бастапқы шарт деп атайды. Әрине, мұнда .

Бұл жерде де Коши есебіне геометриялық, механикалық мән беруге болады. Бірақ, теңдеудің реті жоғары болған сайын бастапқы шартқа мән-мағына беру қиынға соғады. Мысалы, екінші ретті теңдеу үшін қойылған бастапқы екі мәннің біріншісі, шешімнің қай нүкте арқылы өтетінін білдірсе, екіншісі, интегралдық қисықтың сол нүктедегі жанамасының 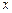өсімен жасайтын бұрыштың тангенсін білдіреді, ал механикалық жағынан – қозғалыстың берілген қалыптан қандай жылдамдықпен өтетінін білдіреді.

1.2. Жоғарғы ретті теңдеулердің қасиеттерін зерттегенде оларды бірінші ретті теңдеулер жүйесіне келтіріп алу ыңғайлы.

Берілген (2) теңдеу үшін мынандай белгілеулер енгізейік:

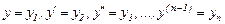
Бұл жағдайда (2) теңдеудің орнына мынандай жүйе аламыз:

(4)

Бұл жүйе жалпы қалыпты

(5)

жүйенің дербес түрі. Сондықтан, алда біз (5) түрдегі қалыпты жүйелерді қарастырамыз.

Жалпы, бірінші ретті теңдеулердің қалыпты жүйесін ретті бір теңдеуге келтіруге болады. Ол үшін (5) жүйенің бір теңдеуін 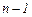рет дифференциалдап, сол жүйенің басқа теңдеулерін пайдаланып отыру керек (мұнда функциялары керекті рет дифференциалданады деп алу керек). (5) жүйенің бірінші теңдеуін алып 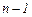рет дифференциалдайық:

(6)

Егер 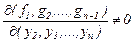, онда (5) жүйенің бірінші теңдеуінен және (6) жүйенің алдыңғы - теңдеуінен құрылған жүйені 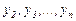бойынша шешуге болады және олар арқылы өрнектеледі.

Осы табылған 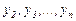өрнектерін (6) жүйенің соңғы теңдеуіне апарып қойсақ,

(7)

түріндегі ретті бір теңдеу аламыз. (5) жүйе мен (7) теңдеудің интегралдық қисықтары бір болады.

1.3. Енді (5) түрдегі қалыпты жүйелерге байланысты кейбір түсініктерді келтірейік.

Алдымен, бұл жүйелерді векторлық функциялар енгізу арқылы қысқартып жазуға болады.

Егер және деп алсақ, онда (5) жүйені былай жазамыз:

(8)

Бұл қатынасты векторлық бір теңдеу деп те, қалыпты жүйе деп те атауға болады. Мұндағы, - вектор-функциясы кейбір облысында анықталған үздіксіз функция. Бұл жүйенің шешімін де алдыңғы анықтамаларға ұқсас түрде анықтайды.

Анықтама-3. аралығында анықталған вектор-функциясы (8) жүйенің шешімі деп аталынады, егер ол төмендегідей үш шартты қанағаттандырса:

1) функциясы аралығында дифференциалданатын

болса;

2) ;

3) .

Айталық, вектор-функциясы (8) жүйенің аралығында анықталған шешімі болсын. кеңістігіндегі - нүктелердің жиыны берілген жүйенің интегралдық қисығын береді, ал кеңістігіндегі - нүктелердің жиыны жүйенің траекториясын береді. Осы кеңістігі фазалық кеңістік деп аталынады. Белгілі бір шешімге сәйкес траектория сол шешімнің кеңістігіндегі интегралдық қисықтың кеңістігіне 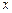өсіне параллель түсірілген көлеңі (проекциясы) болып табылады.

Векторлық (8) теңдеу үшін Коши есебі былай қойылады: барлық шешімдердің ішінен

(9)

шартты қанағаттандыратын шешімін табу керек. Мұнда - бастапқы вектор, - бастапқы нүкте.

Бұл Коши есебіне жауапты төмендегідей теорема айқындайды.

Теорема-1. Егер функциясы бастапқы нүктені қамтитын ашық облысында үздіксіз болса, ал оның кез келген шектелген тұйық ішкі бөлігінде 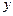векторы ьойынша Липшиц шартын қанағаттандыратын болса, онда Коши есебінің кейбір кішірейген аралықта анықталған жалғыз ғана шешімі болады.

Бұл теореманы глобалды теорема дейді. Біз теореманың дәлелдеуін келтірмейміз (оны [5] оқулықтан көруге болады).

Шешімнің басқада қасиеттерін білдіретін кейбір тұжырымдарды қысқаша түрде дәлелдеусіз келтіре кетейік.

Теорема-2. Егер (8) теңдеу үшін 1-теореманың шарттары орындалса, онда Коши есебін қанағаттандыратын шешім бастапқы мәндер бойынша үздіксіз болады.

Теорема-3. Егер (8) теңдеудің оң жағындағы функция қосымша кейбір параметрлерге байланысты болса және сол параметрлер бойынша үздіксіз болса, онда Коши есебін қанағаттандыратын шешім параметрлер бойынша да үздіксіз болады.

Бұл теоремалардың да дәлелдеулерін жоғарыда көрсетілген оқу құралынан алуға болады.

1.4. Қалыпты (8) жүйедегі вектор-функциясы кейбір ашық (не тұйық) облысында шешімнің бар болу және жалғыздық шарттарын қанағаттандырсын. Осы 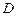облысты шешімнің бар болу және жалғыздық облысы деп атайды.

Анықтама-4. 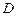облысында анықталған, тәуелсіз айнымалы бойынша үздіксіз дифференциалданатын, тұрақты векторы бойынша үздіксіз

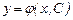(10)

функциясы (8) жүйенің жалпы шешімі деп аталынады, егер ол төмендегідей екі шартты қанағаттандырса:

1) оны тұрақты 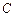векторы бойынша шешуге болатын

болса, яғни

(11)

2) тұрақты 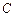векторының (11) формула бойынша

анықталған барлық мәндерінде (10) қатынас (8) жүйенің шешімі болса.

Бұл анықтама Коши есебінің шешімін табу жолын көрсетеді.

Егер (8) жүйе үшін

бастапқы шарты қойылса, онда (11) қатынастан:

Осы векторын (10) қатынасқа қойсақ,

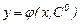
түріндегі Коши есебінің шешімін аламыз.

Анықтама-5. 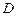облысында анықталған, өздігінен тұрақты санға айналмайтын, үздіксіз дифференциалданатын функциясы (8) жүйенің интегралы деп аталады, егер ол функция 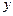векторының орнына (8) жүйенің кез келген шешімін қойғанда тұрақты санға тепе-тең болса.

Осы функцияны еркін тұрақты санға теңестіру арқылы алынған

(12)

қатынасты жүйенің бірінші интегралы деп атайды.

Интегралдың бір қасиетін айта кетейік, - үздіксіз диффренциалданатын функция болсын.

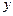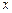Айталық, бірінші интегралдағы -тің орнына (8) жүйенің бір дербес шешімі қойылған деп. Бұл жағдайда функциясы тек айнымалысынан ғана тәуелді болады. Осы функцияны 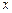бойынша дифференциалдасақ, онда (12) қатынастан

тепе-теңдігін аламыз. Бұдан

тепе-теңдігі алынады. Бұдан шығатын қорытынды – жүйе бойынша алынған интегралдың толық туындысы нөлге тепе-тең, яғни

Осыдан

Кей жағдайда интегралдың бұл қасиетін оның анықтамасы ретінде қолданады.

Қалыпты жүйенің бірінші интегралдары белгілі болса, онда олар жүйенің жалпы шешімін береді.

Жалпы шешімнен 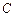векторының белгілі бір мәнінде шығатын шешімді дербес шешім дейді, ал 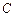векторының тұрақты мәндерінде алынбайтын шешімді ерекше шешім дейді. Бұл түсініктерді басқаша да беруге болатынын 1-тарауда айтқанбыз: әрбір нүктесінде Коши есебінің жалғыздық шарты орындалатын шешімді дербес шешім, ал әрбір нүктесінде Коши есебінің жалғыздық шарты орындалмайтын шешімді ерекше шешім дегенбіз.

Ерекше шешімдер әдетте, теңдеудің оң жағындағы функцияның 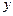бойынша алынған туындыларының шексіздікке айналатын нүктелер жиыны ішінен ізделінеді.