Дәлелдеуі

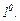Алдымен Коши есебінің интегралдық теңдеуге пара-пар екендігін көрсетейік.

Айталық, 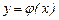функциясы (2) шартты қанағаттандыратын,

кесіндісінде анықталған (1) теңдеудің шешімі болсын:

Соңғы тепе-теңдікті х₀ -ден х -қа дейін интегралдасақ, мынандай тепе-теңдік аламыз:

Бұдан 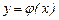функциясының

(5)

интегралдық теңдеудің шешімі болатынын көреміз.

Енді керісінше, 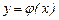функциясы (5) теңдеудің шешімі болсын:

Бұдан болатынын көреміз. Егер осы тепе-теңдікті дифференциалдасақ,

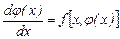
тепе-теңдігін аламыз.

Бұдан шығатын қорытынды – Коши есебінің шешімін табу үшін

интегралдық теңдеудің шешімінің барлығын және жалғыздығын дәлелдесек жеткілікті.

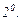Интегралдық теңдеудің шешімін біртіндеп жуықтау әдісімен іздейміз. Бұл әдісті Пикар әдісі деп те атайды.

Бастапқы нөлдік жуықтау ретінде ізделініп отырған функцияның алғашқы y₀ мәнін аламыз да, бірінші жуықтау үшін

(6)

өрнегін жазамыз, ал екінші жуықтау үшін

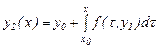(7)

өрнегін жазамыз. Жалпы, кез келген -ші жуықтауды мына түрде жазамыз:

(8)

Мұнда . Осы кесіндіні Пеано кесіндісі деп атайды.

Енді алынған {y_n} тізбегінің әрбір мүшесі берілген облыстың ішінде жататынын көрсетуіміз керек. Айнымалы 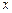-ты Пеано кесіндісінде өзгереді деп, жуықтаулардың бастапқы мәннен ауытқуларын есептейік.

Алдымен,

Екінші жуықтау үшін:

Жалпы, кез келген -ші жуықтау үшін төмендегідей теңсіздік аламыз:

(9)

Бұл теңсіздіктер тізбектің барлық мүшелері D облысының кейбір кішірейген облысының ішінде жататынын көрсетеді.

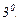Енді жуықтаулар тізбегінің жинақтылығын көрсетейік. Тізбектің жинақтылығын дәлелдеу үшін сол тізбектен құрылған функциялық қатарды қарастырамыз:

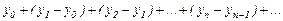(10)

Осы қатар бірқалыпты жинақты болса, онда 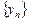тізбегі де бірқалыпты жинақты болады, өйткені, .

Қатардың әрбір мүшесін, екіншісінен бастап, Пеано кесіндісінде абсолют шамасы бойынша бағалайық:

,

Соңғы теңсіздікке Липшиц шартын пайдалансақ, онда

Осылайша,

теңсіздігі алынады. Кез келген -ші мүше үшін де индукция әдісін пайдаланып, төмендегідей теңсіздік аламыз:

Сонымен, функциялық (10) қатардың абсолют шамасынан құрылған қатар Пеано кесіндісінде төмендегідей сандық қатармен бағаланып отыр:

(11)

Бұл қатарды (10) функциялық қатардың мажоранты деп атайды.

Енді осы мажоранттық қатардың жинақтылығын көрсетейік. Даламбер белгісіне сүйенсек,

,

яғни, (11) қатар жинақты. Сондықтан, Вейерштрасс теоремасы бойынша функциялық (10) қатар Пеано кесіндісінің ішінде бірқалыпты абсолютты жинақты. Егер қатардың қосындысын деп белгілесек, онда тізбектің шегі осы болады:

(10) қатардың әрбір мүшесі кесіндінің ішінде үздіксіз функция болғандықтан және ол қатар бірқалыпты жинақты болғандықтан, Коши теоремасы бойынша осы кесіндінің ішінде функциясы да үздіксіз болады.

Тізбектің бірқалыпты жинақтылығынан шарты шығады. Липшиц шартын пайдаланып,

теңсіздігін аламыз. Бұл теңсіздік интегралдан шек алу үшін сол интеграл астындағы өрнектен шек алуға болатынын көрсетеді, яғни

Осыны пайдаланып, (8) қатынастан шек алайық: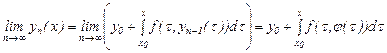

немесе

(12)

Бұл тепе-теңдіктен j(x) функциясының Пеано кесіндісінде интегралдық теңдеудің шешімі болатынын көреміз. Сондықтан, ол Коши есебінің шешімін береді.

Коши есебінің шешімінің жалғыздығын дәлелдеу үшін алдымен Гронуолл леммасын келтірейік.

Лемма. Кейбір 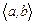аралығында үздіксіз функциялары және тұрақты саны үшін

(13)

теңсіздігі орындалса, онда одан мынандай теңсіздік алуға болады:

(14)

Дәлелдеуі. (13) теңсіздікті оң жағындағы қосындыға бөлейік :

Екі жағында оң функциясына көбейтіп, 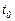-ден -ға дейін интеграл алайық:

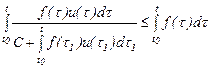
Мұнда бөлшектің алымы бөлімінің туындысы екенін ескерсек, онда

Осыдан

Потенциалдап, одан соң берілген (13) теңсіздікті пайдалансақ, (14) теңсіздікке келеміз ( болғанда лемманы дәлелдеу үшін интегралдың бағытын өзгертсе, жеткілікті).

Енді осы (14) теңсіздікті пайдаланып, шешімнің жалғыздығын көрсетейік.

Айталық, j(x) және ψ (x) функциялары әртүрлі екі шешім болсын:

,

Осы шешімдердің айырмасын бағалайық:

Мұнда , f(x)=L, C=0 екенін ескерсек, (14) теңсіздіктен теңдігі шығатынын көреміз, яғни j(x)=ψ(x), .

Сонымен, Пеано кесіндісінде Коши есебінің тек жалғыз ғана шешімі бар екені толық дәлелденді.

Ескерту-1. Шешім кесіндісінде анықталып отыр. Мұнда , яғни саны М санына кері тәуелді: М саны үлкен болса, аз сан болады. Сондықтан, шешім нүктесінің қысқа тұйық аумағында анықталып отыр. Осы себепті бұл тұжырымды локалды теорема деп атайды. Ал шындығында, шешімді берілген облыстың шекарасына дейін созуға болады.

Ескерту-2. Әдетте, Липшиц шартының орнына одан басымырақ және оңай тексерілетін шарт алынады. Дәлірек, 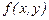функциясы берілген тұйық облыста у аргументі бойынша үздіксіз дифференциалданады – деп.

Бұл шарт орындалғанда Липшиц шарты өзінен өзі орындалады.