Уравнения эллиптического типа

ЗАДАЧА 10. Поставить задачу об определении температуры тонкой однородной пластинки с теплоизолированными основаниями при условии, что температура не зависит от времени (стационарное тепловое поле). Рассмотреть случаи:

а) на границе пластинки поддерживается заданная температура;

б) через границу пластинки подается извне заданный тепловой поток;

б¢) граница теплоизолирована;

в) через границу пластинки проходит теплообмен по закону Ньютона со средой, температура которой известна.

Решение. Совместим одно из оснований пластинки с плоскостью xоy; ввиду малой толщины пластинки, можно предполагать, что температура является функцией переменных , т.е. .

Пусть - часть пластинки, ограниченная кривой 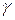(точнее, - прямой цилиндр с направляющей 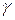). Количество тепла, которое получит область через границу за единицу времени, согласно закону Фурье, равно

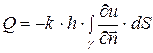, (2.22)

где 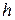- высота пластинки. Так как температура не меняется со временем, то и, следовательно,

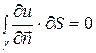. (2.23)

Применяя формулу Грина, получим

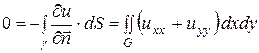, (2.24)

причем это соотношение справедливо для произвольной области G. Предполагая, что частные производные 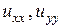непрерывны из равенства (2.24) получим

. (2.25)

Итак, стационарная температура в пластинке удовлетворяет уравнению Лапласа (2.25).

Вывод граничных условий. Обозначим через C границу пластинки. Граничное условие в случае а), очевидно, имеет вид

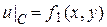, (2.26)

где 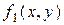- заданная температура на границе пластинки.

В случае б) поступаем следующим образом. Пусть 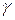- произвольная дуга кривой С; проведем через концы дуги 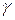отрезк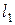и и внутренних нормалей длины и соединим их концы дугой 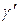, параллельной 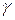. Подсчитаем количество тепла , которое получит четырехугольник, ограниченны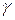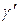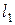й , , и , через свою границу за единицу времени. Обозначая через плотность заданного теплового потока через границу 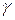пластинки, получим

, (2.27)

где и 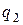- потоки тепла через границы 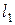и .

В равенстве (2.27) переходя к пределу при 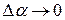и, учитывая, что , , , 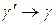получим

(2.28)

В силу произвольности 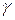подынтегральное выражение тождественно равно нулю на C,и мы приходим к граничному условию

, (2.29)

где .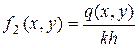

Так как суммарный поток тепла через границу C должен быть нулем, то функция 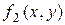должна удовлетворять условию

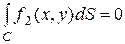. (2.30)

В случае б¢) имеем 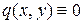и условие (2.29) принимает вид:

. (2.31)

Случай в) следует из случая б) при , где 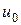- температура окружающей среды. Граничное условие имеет вид

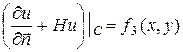, где 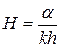, 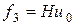. (2.32)

Итак, задача формулируется следующим образом. Найти функцию 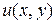, непрерывную в замкнутой области так, чтобы она удовлетворяла уравнению (2.25) в и одному из граничных условий (2.26), (2.29), (2.31), (2.32). Задача с граничным условием (2.26) называется задачей Дирихле, а с граничным условием (2.29) – задачей Неймана.

Замечание 1. В задачи № 1-9 входят как граничные, так и начальные условия; такие задачи называются смешанными.

В задачи № 10 входят лишь граничные условия; такие задачи называются граничными или краевыми задачами; они типичны для уравнения Лапласа.

На практике встречаются также задачи с одними начальными условиями; задача такого типа называется задачей Коши. Обычно при постановке задачи Коши считают, что пространственные переменные изменяются в бесконечных пределах.

В качестве примера задачи Коши можно привести задачу о колебании бесконечной струны.

Найти функцию , непрерывную в области , 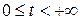так, чтобы она удовлетворяла уравнению

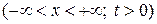, (2.33)

и начальным условиям

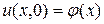, , . (2.34)

«Бесконечная струна» - это идеализация достаточно длинной струны.

ОТВЕТЫ К ЗАДАЧАМ

Задача 2 .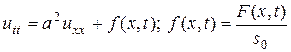

,

.

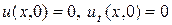Задача 3 ;

,

.

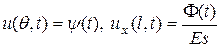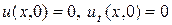Задача 5 ;

,

Задача 6 ;

,

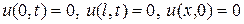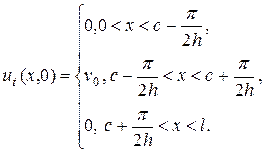
Задача 8 Уравнение теплопроводности в данном случае имеет вид

,

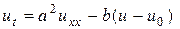где Р – периметр поперечного сечения, 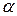- коэффициент теплообмена между поверхностью стержня и окружающей средой, температура которой равна 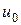; остальные величины такие же, как в условии задачи 7.