 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение уравнения Лапласа методом разделения переменных
|
|
ЗАДАЧА 15. Найти решение первой граничной задачи (задачи Дирихле) для уравнения Лапласа внутри прямоугольника: 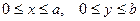 при произвольных граничных условиях.
при произвольных граничных условиях.
Задача Дирихле состоит в нахождении функции  , непрерывной в замкнутом прямоугольнике
, непрерывной в замкнутом прямоугольнике 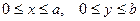 , по условиям:
, по условиям:
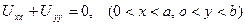 , (1.33)
, (1.33)
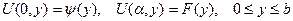 , (1.34)
, (1.34)
 , (1.35)
, (1.35)
причем
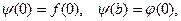
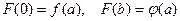 . (1.36)
. (1.36)
Последние условия обеспечивают непрерывность граничной функции в вершинах прямоугольника.
Решение. Не нарушая общности, можно предполагать, что все значения в (1.36) равны нулю, так как к этому случаю можно привести любую задачу. Для этого надо представить решение в виде
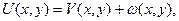
где 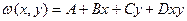
при 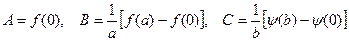 ,
,
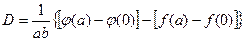 .
.
Для функции 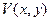 получим задачу Дирихле при нулевых значениях в вершинах прямоугольника. Итак, будем решать задачу (1.33) –(1.36), предполагая, что все значения в (1.36) есть нули.
получим задачу Дирихле при нулевых значениях в вершинах прямоугольника. Итак, будем решать задачу (1.33) –(1.36), предполагая, что все значения в (1.36) есть нули.
Представим решение в виде
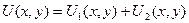 , (1.37)
, (1.37)
где 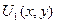 и
и 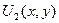 удовлетворяют уравнению Лапласа и следующим граничным условиям:
удовлетворяют уравнению Лапласа и следующим граничным условиям:
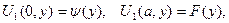 (1.38)
(1.38)
 , (1.39)
, (1.39)
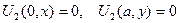 , (1.40)
, (1.40)
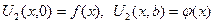 . (1.41)
. (1.41)
(При сделанном предложении непрерывность граничных значений сохранена).
Функции 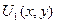 и
и 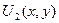 можно найти методом разделения переменных. Проведем решение для функции
можно найти методом разделения переменных. Проведем решение для функции 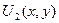 .
.
Ищем частные решения уравнения Лапласа, удовлетворяющие условиям (1.40) вида
 . (1.42)
. (1.42)
Подстановка (1.42) в (1.33) дает 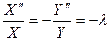
или 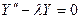 , (1.43)
, (1.43)
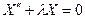 . (1.44)
. (1.44)
Подстановка (1.42) в (1.40) дает
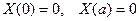 . (1.45)
. (1.45)
Задача Штурма - Лиувилля (1.44), (1.45) имеет решение:
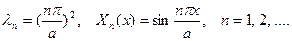
Общее решение уравнения (1.43) при 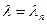 можно записать в виде
можно записать в виде
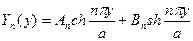 .
.
Общее решение задачи ищем, как обычно, в виде ряда
 . (1.46)
. (1.46)
Удовлетворим теперь граничным условиям (1.39), которые содержат заданные произвольные функции:
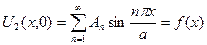 ,
,
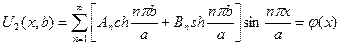 ,
,
откуда получаем 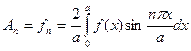 ,
,
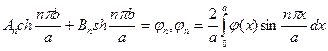 ,
,
и, наконец,
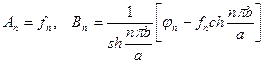 .
.
Подстановка этих значений в (1.46) дает после несложных преобразований
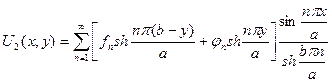 .
.
Совершенно аналогично найдем
 ,
,
где
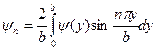 ,
,
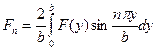 .
.
Окончательное решение:
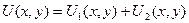 .
.
Дата публикования: 2014-11-02; Прочитано: 2357 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
