 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вывод дифференциального уравнения
|
|
Рассмотрим элемент стержня  (рис.2.3).
(рис.2.3).
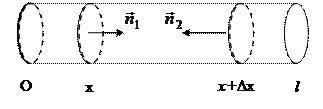 |
Рис.2.3
Так как боковая поверхность стержня теплоизолирована, то элемент  может получать тепло только через поперечные сечения
может получать тепло только через поперечные сечения 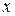 и
и 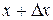 . Обозначим через
. Обозначим через  площадь поперечного сечения, а через
площадь поперечного сечения, а через 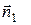 и
и 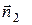 - нормали к сечениям
- нормали к сечениям 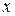 и
и 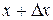 , направленные внутрь элемента
, направленные внутрь элемента  . Тогда по закону Фурье тепло, поступившее в элемент за время
. Тогда по закону Фурье тепло, поступившее в элемент за время 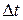 через сечения
через сечения 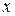 и
и 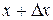 , запишется соответственно в виде
, запишется соответственно в виде  ,
,
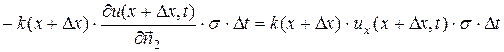 ;
;
при этом мы учли, что направление 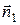 совпадает с направлением оси Ox, а направление
совпадает с направлением оси Ox, а направление 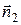 противоположно ему. Складывая последние выражения и применяя теорему о конечных приращениях, запишем общее количество тепла, полученное элементом за время
противоположно ему. Складывая последние выражения и применяя теорему о конечных приращениях, запишем общее количество тепла, полученное элементом за время 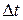 в виде
в виде
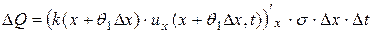 ,
, 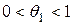 .
.
По закону сохранения энергии все это тепло идет на нагревание элемента, поэтому его можно выразить формулой (2.7)
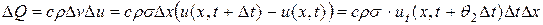 ,
, 
Приравнивая оба выражения для  и сокращая на
и сокращая на 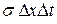 , затем переходя к пределу при
, затем переходя к пределу при 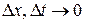 , получим дифференциальное уравнение теплопроводности
, получим дифференциальное уравнение теплопроводности 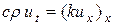 .
.
Если стержень однородный, т.е. 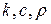 - постоянные, то уравнение можно записать в виде
- постоянные, то уравнение можно записать в виде
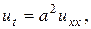
 , (2.10)
, (2.10)
где 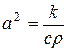 .
.
Начальное условие имеет вид 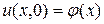 , (
, (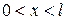 ), (2.11)
), (2.11)
где 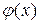 - начальное значение температуры.
- начальное значение температуры.
Приступаем к выводу граничных условий. Очевидно, имеем
а) 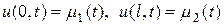 , (2.12)
, (2.12)
где 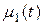 и
и 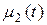 - температуры концов стержня.
- температуры концов стержня.
В случае б) проводим те же рассуждения, что и при выводе уравнения (2.10), для граничных элементов 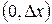 и
и 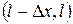 .
.
Обозначим через 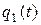 количество тепла, поступающего в единицу времени через сечение
количество тепла, поступающего в единицу времени через сечение 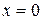 . Тогда уравнение теплового баланса для элемента
. Тогда уравнение теплового баланса для элемента 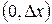 запишется в виде
запишется в виде
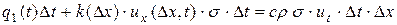 .
.
Сократив на 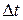 и перейдя к пределу при
и перейдя к пределу при 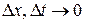 , получим
, получим
б) 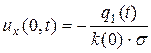 . (2.13)
. (2.13)
Совершенно аналогично получаем
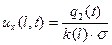 , (2.14)
, (2.14)
где  - поток тепла через сечение
- поток тепла через сечение 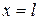 .
.
В случае теплоизолированных концов 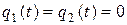 и, следовательно:
и, следовательно:
б’) 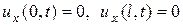 (2.15)
(2.15)
Наконец, случай теплообмена в) можно рассматривать как частный случай случая б) при 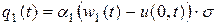 ;
;
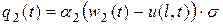 ;
;
(см. закон Ньютона), где 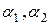 - коэффициенты теплообмена, а
- коэффициенты теплообмена, а  - температуры среды у концов стержня. После этого получаем из (2.13), (2.14):
- температуры среды у концов стержня. После этого получаем из (2.13), (2.14):
в) 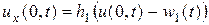 (2.16)
(2.16)
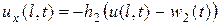 , где
, где 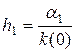 ,
, 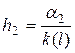 . (2.17)
. (2.17)
Итак, задача формулируется следующим образом. В области 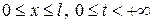 найти непрерывную функцию
найти непрерывную функцию 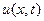 так, чтобы она удовлетворяла уравнению (2.10), начальным условиям (2.11) и граничным условиям одного из типов (2.12), (2.13), (2.14), (2.15) или (2.16), (2.17).
так, чтобы она удовлетворяла уравнению (2.10), начальным условиям (2.11) и граничным условиям одного из типов (2.12), (2.13), (2.14), (2.15) или (2.16), (2.17).
ЗАДАЧА 8. Поставить задачу об определении температуры стержня при начальных и граничных условиях предыдущей задачи для случая, когда на боковой поверхности стержня происходит теплообмен по закону Ньютона со средой, температура которой является заданной функцией времени.
Указание. Дифференциальное уравнение и граничные условия выводятся так же, как в задаче 7, но надо учесть, что теперь тепло поступает в элемент не только через его торцы, но и через боковую поверхность.
ЗАДАЧА 9. Вывести уравнение для температуры тонкой проволоки, нагреваемой постоянным электрическим током, если на еe поверхности происходит конвективный теплообмен по закону Ньютона с окружающим воздухом, имеющим известную температуру.
Поставить задачу об определении температуры в этом проводе, если концы его зажаты в массивные клеммы с заданной теплоемкостью и очень большой теплопроводностью.
Решение. Дифференциальное уравнение выводится так же, как и в задаче 7, только теперь к количеству тепла, которое получает элемент проволоки  через торцы и боковую поверхность, надо прибавить количество тепла, которое выделяется в элементе электрическим током за время
через торцы и боковую поверхность, надо прибавить количество тепла, которое выделяется в элементе электрическим током за время 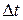 :
: 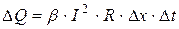 , где
, где 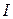 - сила тока,
- сила тока, 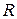 - сопротивление единицы длины провода,
- сопротивление единицы длины провода, 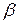 - коэффициент пропорциональности.
- коэффициент пропорциональности.
Указанное дифференциальное уравнение имеет вид
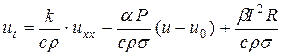 , (2.18)
, (2.18)
где 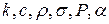 - имеют тот же смысл, что и в задаче 8 (см. ответ). Начальное условие, как и в задачах 7 и 8, имеет вид
- имеют тот же смысл, что и в задаче 8 (см. ответ). Начальное условие, как и в задачах 7 и 8, имеет вид 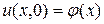 , (2.19)
, (2.19)
где 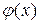 - температура проволоки при
- температура проволоки при 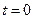 .
.
Выведем граничные условия.
Рассмотрим тело T, состоящее из граничного элемента 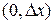 и примыкающей к нему клеммы. Это тело получает тепло через сечение
и примыкающей к нему клеммы. Это тело получает тепло через сечение 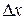 , через боковую поверхность элемента и в результате прохождения тока через элемент (теплом, которое выделяет ток в клемме и которое теряется клеммой в результате теплообмена можно пренебречь). Суммарное количество тепла, получаемого телом T, составит
, через боковую поверхность элемента и в результате прохождения тока через элемент (теплом, которое выделяет ток в клемме и которое теряется клеммой в результате теплообмена можно пренебречь). Суммарное количество тепла, получаемого телом T, составит
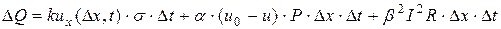 .
.
Это тепло идет на изменение температуры тела T и, следовательно, равно
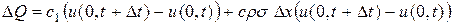 ,
,
при этом мы считаем, что температура во всех точках тела T постоянна, так как 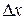 мало, а клемма обладает очень большой теплопроводностью. Приравнивая эти значения
мало, а клемма обладает очень большой теплопроводностью. Приравнивая эти значения 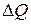 , деля результат на
, деля результат на 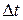 и переходя к пределу при
и переходя к пределу при 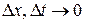 , получим
, получим
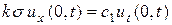 . (2.20)
. (2.20)
Совершенно аналогично получим условие на другом конце:
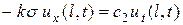 , (2.21)
, (2.21)
где 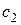 - теплоемкость клеммы на конце
- теплоемкость клеммы на конце 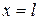 .
.
Дата публикования: 2014-11-02; Прочитано: 1187 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
