Решение задач свободных и вынужденных колебаний методом разделения переменных

ЗАДАЧА 11. Проинтегрировать уравнение малых продольных колебаний цилиндрического стержня при условии, что один конец 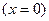закреплен жестко, а другой 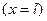свободен.

Решение. Задача ставится следующим образом (см. задачу №1):

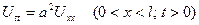. (1.1)

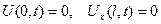. (1.2)

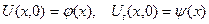. (1.3)

Частные решения ищем в виде

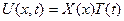. (1.4)

Уравнения для 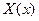и 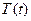будут, очевидно, те же, что и в задаче №24:

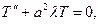(1.5)

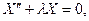(1.6)

но граничные условия для 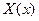будут другие:

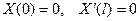. (1.7)

Как и в предыдущих задачах, легко убедиться в том, что при 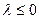задача (1.6), (1.7) решения не имеет. При 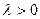решение уравнения (1.6) есть

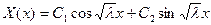. (1.8)

Подставляя его в (1.7), получим ,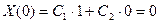

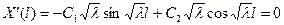. (1.9)

Приравнивая определитель системы (1.9) к нулю, получим

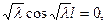
откуда

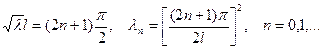
Из (1.9) имеем далее 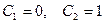, после чего из (1.8) получим

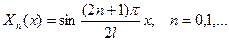(1.10)

Найдя теперь общее решение уравнения (1.5), при 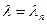получим

.

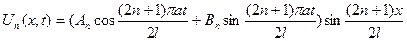Общее решение будет

.

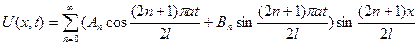Подстановка в начальные условия дает

,

.

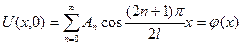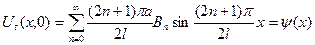Коэффициенты 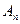находим согласно формулам (1.7)

.

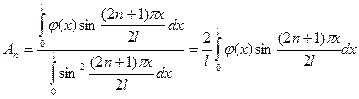Аналогично находим

.

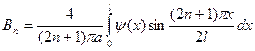ЗАДАЧА 12. Исследовать свободные колебания закрепленной струны, колеблющейся в среде, сопротивление которой пропорционально первой степени скорости.

Решение. Дифференциальное уравнение в данном случае имеет вид

,

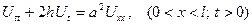где 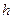– малое положительное число; остановимся на случае, когда ;

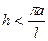начальные условия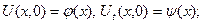

граничные условия .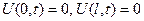

Имеем:

, , ,

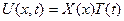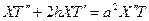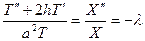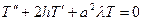, (1.11)

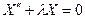, (1.12)

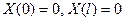, (1.13)

Решение задачи (1.12), (1.13) есть

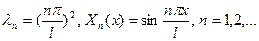
При 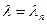дифференциальное уравнение (1.11) примет вид

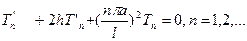
Его характеристическое уравнение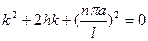

имеет корни .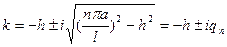

Следовательно, общее решение этого дифференциального уравнения имеет вид

.

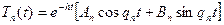Общее решение задачи запишем в виде

.

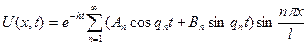Подставляя его в начальные условия, получим

,

,

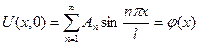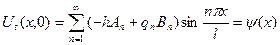откуда ,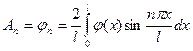

.

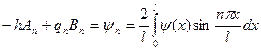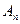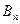Решая эту систему относительно и , получим .

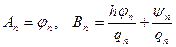ЗАДАЧА 13. Решить задачу, поставленную в № 2.

Постановки задачи. Требуется найти решение уравнения (1.14), удовлетворяющее граничным условиям (1.15) и начальным условиям (1.16).

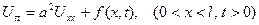, (1.14)

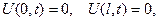(1.15)

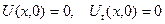. (1.16)

Решение. Для того чтобы построить общее решение уравнения (1.14), удовлетворяющее условиям (1.15), надо знать собственные функции задачи Штурма - Лиувилля, к которой приводится решение соответствующего однородного уравнения

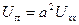
при тех же граничных условиях (1.15).

Эти собственные функции имеют вид: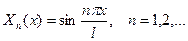

Общее решение задачи (1.14), (1.15), (1.16) ищем в виде ряда по этим собственным функциям:

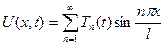, (1.17)

где 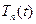– функции, подлежащие определению.

Подставляя (1.17) в (1.14), получим

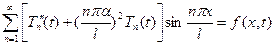. (1.18)

Предполагая, что функция 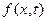удовлетворяет теореме Стеклова по переменной 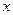, заключаем, что тождество (1.18) будет выполнено, если:

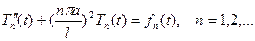(1.19)

где

.

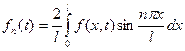Подставляя (1.17) в начальные условия (1.16), получим

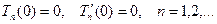(1.20)

Решение уравнения (1.19) вместе с условиями (1.20) имеет вид

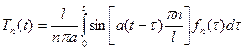. (1.21)

Оно может быть найдено методом вариации произвольных постоянных. Решение задачи дается рядом (1.17), где функция 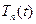определена соотношением (1.21).