 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Оригинал и изображение
|
|
Мы переходим к изучению метода преобразования Лапласа (операционного исчисления), получившего распространение немногим более полувека назад. В настоящее время преобразование Лапласа (операционное исчисление) приобрело широкую известность приложениями к вопросам физики и техники, став, например, основным методом решения задач теории переходных процессов в электрических цепях и теории теплопроводности.
Оригиналом мы будем называть любую комплексную функцию f(t) действительного аргумента t, определенную на всей числовой оси и удовлетворяющую условиям:
1) f(t) непрерывнана всей оси t за возможным исключением точек разрыва первого рода в конечном числе точек на каждом интервале конечной длины;
2) f(t) =0 при t <0;
3) существуют числа М>0 и s0≥0 такие, что для всех t
 (2.1)
(2.1)
Если для s0 выполняется условие  , то оно будет выполняться и для всех s>so, так как
, то оно будет выполняться и для всех s>so, так как 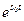 <
< 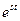 при t>0.
при t>0.
Число so, для которого выполняется условие (2.1) назовем показателем роста функции f (t). 
Так, например, для ограниченной функции число 0 является показателем роста.
В силу условия 1 оригиналы, ни при каком значении t не обращаются в бесконечность. Следовательно, функции 
 или tg t не являются оригиналами и из рассмотрения исключаются.
или tg t не являются оригиналами и из рассмотрения исключаются.
Условие 2, требующее обращения оригиналов в нуль при t<0, практически не является стеснительным, так как при решении дифференциальных уравнений, соответствующих физическим задачам (а для этого вообще говоря, и строится операционное исчисление), интересующими нас значениями функций являются значения, начиная с момента, данного в начальном условии, а за таковой всегда можно принять момент t=0.
Для краткости мы будем записывать лишь то выражение оригинала f (t), которое он имеет при t≥0, но нужно помнить об условии 2. Так что, если написано f (t)= t3, то это нужно понимать так 
Условие 3 требует, чтобы оригиналы при t→ ∞ были или ограничены или стремились к бесконечности, но не быстрее, чем показательная функция вида (2.1). Так, например, функция  не является оригиналом, так как при t→ ∞ растет быстрее, чем разрешает условие 3.
не является оригиналом, так как при t→ ∞ растет быстрее, чем разрешает условие 3.
Изображением функции f (t) называют функцию комплексной переменной 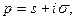 определяемую соотношением
определяемую соотношением
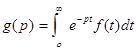 (2.2)
(2.2)
Интеграл в правой стороне этого равенства называют интегралом Лапласа. Операцию перехода от оригинала f(t) к изображению g(p) называют преобразованием Лапласа. Фразу «оригинал f(t) имеет изображением g(p)» записывают символически
 или
или 
Операционным исчислением мы будем называть теорию преобразования Лапласа.
Практическая ценность операционного исчисления состоит, как выяснится в дальнейшем, в том, что дифференцированию оригиналов соответствует умножение их изображений на p, а интегрированию оригиналов – деление их изображений на p, то есть сложным операциям над оригиналами соответствуют простые операции над их изображениями.
С подобным положением мы сталкивались в теории логарифмов, где операции умножения чисел соответствовала операция сложения их логарифмов, то есть более сложной операции над числами соответствовала более простая операция над их логарифмами.
Это обстоятельство предопределяет и аналогию между схемами практических приложений логарифмов и операционного исчисления к решению уравнений.
Схема применения логарифмов такова:
1) от чисел и неизвестных величин переходят к их логарифмам;
2) совершают соответствующие более простые
действия над логарифмами, находя значение логарифма неизвестной величины;
3) по найденному логарифму искомой величины находят эту величину.
Схема применения операционного исчисления аналогична:
1) переходят от данных функций к их изображениям;
2) совершают соответствующие более простые операции над полученными изображениями, находя изображение искомой функции;
3) по найденному изображению искомой функции находят оригинал.
Схема применения логарифмов реализуется с помощью таблиц чисел и их логарифмов; схема применения операционного исчисления реализуется с помощью таблиц оригиналов и их изображений.
Таблицы логарифмов составляются, как известно из курса анализа, с помощью приближенных вычислений сумм степенных рядов. Таблицы изображений составляются или непосредственно на основе их определения интегралом Лапласа, или с помощью теорем операционного исчисления, рассматриваемых ниже. Приведем примеры непосредственного получения изображений.
Пример 1. Будем называть единичной функцией  функцию, определенную так:
функцию, определенную так: 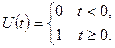
График этой разрывной функции изображен на рисунке 29.
 Она, очевидно, является оригиналом, найдем ее изображение:
Она, очевидно, является оригиналом, найдем ее изображение:
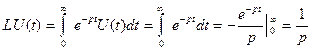 при Rep>0,
при Rep>0,
ибо
 при t→∞.
при t→∞.
Итак, 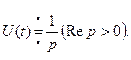
 (2.3)
(2.3)
Пример 2. Найдем изображение оригинала  где q– произвольное комплексное число:
где q– произвольное комплексное число: 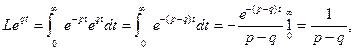
если Re (p-q) > 0, то есть Re p > Re q.
Итак,  . (2.4)
. (2.4)
Пример 3. Найдем изображение оригинала f(t)=cos 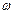 t, где
t, где  – действи–тельное число:
– действи–тельное число:
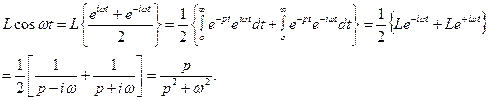
Итак, 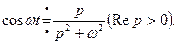
Дата публикования: 2014-11-02; Прочитано: 3937 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
