 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнения гиперболического типа
|
|
ЗАДАЧА 1. Упругий прямолинейный стержень длины 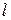 выведен из состояния покоя тем, что его поперечным сечениям в момент времени
выведен из состояния покоя тем, что его поперечным сечениям в момент времени 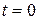 сообщены малые продольные смещения и скорости; предполагая, что поперечные сечения стержня все время остаются плоскими, поставить задачу для определения смещений поперечных сечений стержня при
сообщены малые продольные смещения и скорости; предполагая, что поперечные сечения стержня все время остаются плоскими, поставить задачу для определения смещений поперечных сечений стержня при  . Рассмотреть случаи:
. Рассмотреть случаи:
а) концы стержня закреплены жестко;
а¢) концы двигаются в продольном направлении по заданному закону;
б) к концам приложены заданные силы;
б¢) концы свободны;
в) концы закреплены упруго, т.е. каждый из концов испытывает со стороны заделки продольную силу, пропорциональную смещению и направленную противоположно смещению.
Решение. Идеализация процесса состоит в том, что мы пренебрегаем деформацией поперечных сечений стержня и действием силы тяжести.
Направим ось Ox вдоль стержня и выберем начало координат в левом его конце. За характеризующую функцию возьмем смещение  вдоль оси Ox поперечного сечения, абсцисса которого в состоянии равновесия равна
вдоль оси Ox поперечного сечения, абсцисса которого в состоянии равновесия равна 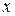 ; как обычно,
; как обычно, 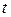 обозначает время.
обозначает время.
Будем считать, что упругие силы, возникающие при продольных деформациях стержня, подчинены закону Гука, т.е.
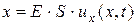 , (*)
, (*)
где 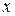 - проекция силы
- проекция силы 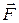 на ось Ox, с которой часть стержня, лежащая правее сечения, абсцисса которого в состоянии равновесия равна
на ось Ox, с которой часть стержня, лежащая правее сечения, абсцисса которого в состоянии равновесия равна 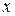 , действует на часть, лежащую левее этого сечения. Сила
, действует на часть, лежащую левее этого сечения. Сила 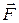 перпендикулярна поперечному сечению и, следовательно, ее направление либо совпадает с направлением оси Ox, либо противоположно ему;
перпендикулярна поперечному сечению и, следовательно, ее направление либо совпадает с направлением оси Ox, либо противоположно ему; 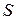 - площадь поперечного сечения;
- площадь поперечного сечения; 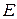 - модуль упругости. Отметим, что закон Гука имеет место в случае, когда колебания достаточно малы.
- модуль упругости. Отметим, что закон Гука имеет место в случае, когда колебания достаточно малы.
Приступаем к выводу дифференциального уравнения. Рассмотрим элемент стержня, торцы которого в состоянии равновесия имеют абсциссы 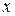 и
и 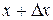 (рис. 2.1).
(рис. 2.1).
 |
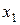
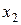
Рис. 2.1
На основании закона Гука, проекции сил упругости 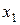 и
и 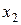 , действующие на элемент со стороны правого и левого торца, соответственно равны
, действующие на элемент со стороны правого и левого торца, соответственно равны 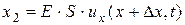 ,
, 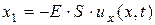 ,
,
а проекция равнодействующей
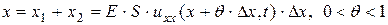 ,
,
здесь мы применили теорему о конечных приращениях.
При достаточно малом 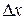 можно рассматриваемый элемент заменить приближенно материальной точкой с массой
можно рассматриваемый элемент заменить приближенно материальной точкой с массой 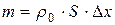 ,
,
где 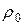 - плотность стержня в невозмущенном состоянии, и записать для него второй закон Ньютона
- плотность стержня в невозмущенном состоянии, и записать для него второй закон Ньютона
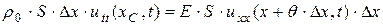 ,
,
где 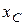 - координата центра тяжести элемента. Сокращая на
- координата центра тяжести элемента. Сокращая на  и переходя к пределу при
и переходя к пределу при 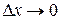 , получим дифференциальное уравнение малых продольных колебаний стержня:
, получим дифференциальное уравнение малых продольных колебаний стержня:
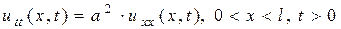 , где
, где 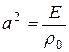 . (2.1)
. (2.1)
Начальные условия задачи запишутся в виде
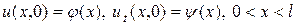 , (2.2)
, (2.2)
где 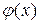 и
и 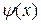 - заданные функции; причем
- заданные функции; причем 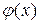 - смещение поперечных сечений стержня, а
- смещение поперечных сечений стержня, а 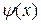 - скорость этих сечений в начальный момент
- скорость этих сечений в начальный момент 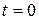 .
.
Приступаем к выводу граничных условий.
Случаи (а) и (а¢) очевидны.
а) 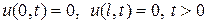 ; (2.3)
; (2.3)
а¢) 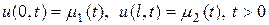 , (2.3¢)
, (2.3¢)
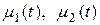 - заданные функции.
- заданные функции.
При выводе граничных условий в случае б) применим те же рассуждения, что и при выводе уравнения (1), с той лишь разницей, что теперь надо рассматривать граничные элементы 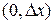 и
и 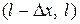 .
.
При этом сила упругости будет приложена к торцу с абсциссой 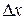 , соответственно
, соответственно 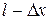 , к концам же стержня приложены внешние силы
, к концам же стержня приложены внешние силы 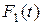 и
и 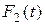 (рис. 2.2).
(рис. 2.2).
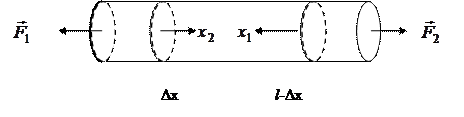 |
Рис. 2.2
Запишем второй закон Ньютона для правого граничного элемента:
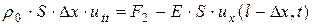 .
.
Переходя здесь к пределу при 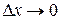 , получим
, получим
б) 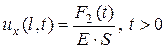 . (2.4)
. (2.4)
Совершенно аналогично получим условие для левого конца:
б¢) 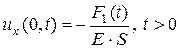 . (2.4¢)
. (2.4¢)
В случае свободных концов 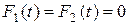 и, следовательно,
и, следовательно,
б¢¢) 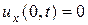 ,
, 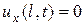 . (2.5)
. (2.5)
Наконец, в случае упругого закрепления
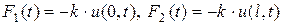 ,
,
где k – коэффициент упругости заделки, после чего получаем из (2.4), (2.4¢)
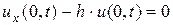 ; (2.6)
; (2.6)
в) 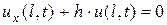 ,
, 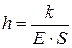 . (2.6’)
. (2.6’)
Задача формулируется так.
В области 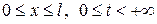 найти непрерывную функцию
найти непрерывную функцию  так, чтобы она удовлетворяла уравнению (2.1), начальным условиям (2.2) и граничным условиям одного из следующих типов (2.3); (2.3¢); (2.4); (2.4¢); (2.5) или (2.6), (2.6¢).
так, чтобы она удовлетворяла уравнению (2.1), начальным условиям (2.2) и граничным условиям одного из следующих типов (2.3); (2.3¢); (2.4); (2.4¢); (2.5) или (2.6), (2.6¢).
ЗАДАЧА 2. На упругий прямолинейный стержень длины 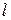 , концы которого закреплены жестко, действует внешняя сила
, концы которого закреплены жестко, действует внешняя сила 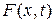 , рассчитанная на единицу его объема и направленная вдоль оси стержня.
, рассчитанная на единицу его объема и направленная вдоль оси стержня.
Поставить задачу о малых продольных колебаниях стержня, если при 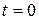 его поперечные сечения были неподвижны и находились в неотклоненном положении.
его поперечные сечения были неподвижны и находились в неотклоненном положении.
Указание. Дифференциальное уравнение выводится так же, как в задаче 1, только надо учесть действие внешней силы.
ЗАДАЧА 3. Начиная с момента 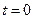 , один конец прямолинейного упругого стержня
, один конец прямолинейного упругого стержня 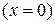 совершает продольные колебания по заданному закону, а к другому
совершает продольные колебания по заданному закону, а к другому 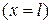 приложена сила
приложена сила 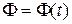 , направленная по оси стержня.
, направленная по оси стержня.
Поставить задачу о малых продольных колебаниях стержня при тех же начальных условиях, что и в задаче 2.
ЗАДАЧА 4. Верхний конец упругого однородного вертикально подвешенного тяжелого стержня жестко прикреплен к потолку свободно падающего лифта, который, достигнув скорости  , мгновенно останавливается.
, мгновенно останавливается.
Поставить задачу о продольных колебаниях этого стержня.
Указание. Направим ось Ox вертикально вниз и примем верхний конец стержня (в момент остановки) за начало координат. Дифференциальное уравнение получим, используя результат задачи 2. В настоящем случае на единицу объема действует внешняя сила 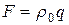 , где
, где 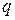 - ускорение силы тяжести,
- ускорение силы тяжести, 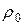 - плотность.
- плотность.
Таким образом, получаем следующее уравнение:
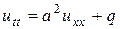 ;
;  .
.
Так как верхний конец 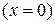 закреплен, а нижний конец
закреплен, а нижний конец 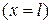 свободен, то граничные условия имеют вид
свободен, то граничные условия имеют вид
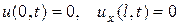 .
.
В момент остановки стержня 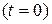 его поперечные сечения находятся в не отклоненном состоянии, но им сообщена постоянная скорость
его поперечные сечения находятся в не отклоненном состоянии, но им сообщена постоянная скорость  , следовательно, начальные условия имеют вид
, следовательно, начальные условия имеют вид
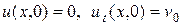 .
.
ЗАДАЧА 5. Поставить задачу о малых поперечных колебаниях струны длины 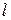 с закрепленными концами, которая оттягивается в точке
с закрепленными концами, которая оттягивается в точке 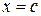 на небольшое расстояние
на небольшое расстояние 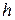 от положения равновесия и в момент времени
от положения равновесия и в момент времени 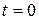 отпускается без начальной скорости.
отпускается без начальной скорости.
Указание. Уравнение малых поперечных колебаний струны имеет вид
 ,
,
где  - отклонение струны от положения равновесия,
- отклонение струны от положения равновесия, 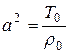 ,
, 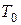 - натяжение струны,
- натяжение струны, 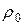 - линейная плотность струны.
- линейная плотность струны.
ЗАДАЧА 6. Однородная струна длины 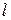 , закрепленная на обоих концах, находится в прямолинейном положении равновесия. В момент
, закрепленная на обоих концах, находится в прямолинейном положении равновесия. В момент 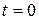 она получает удар от плоского молоточка, имеющего постоянную скорость
она получает удар от плоского молоточка, имеющего постоянную скорость  .
.
Поставить задачу для определения отклонения  струны при
струны при  , если ширина молоточка равна
, если ширина молоточка равна  , а его центр ударяет по точке
, а его центр ударяет по точке 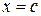 .
.
Дата публикования: 2014-11-02; Прочитано: 2352 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
