Направления выпуклости графика функции одного переменного. Точки перегиба

Пусть функция 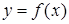имеет конечную или бесконечную производную в каждой точке интервала 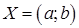. Обозначим дугу графика функции 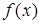, соответствующую интервалу .

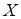Определение. Если дуга лежит не ниже (не выше) касательной к графику функции 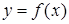, проведенной в любой точке 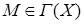, то функция называется выпуклой (соответственно вогнутой) в интервале 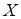(рис. 12 а)).

Точка на графике функции, в которой существует касательная к графику функции, называется точкой перегиба функции или графика функции, если она является границей дуг графика с разными направлениями выпуклости (рис. 12 б,в)).

Заметим, что в точке перегиба требуется существование касательной к графику.

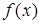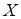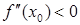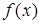Теорема (достаточное условие выпуклости вверх и вниз). Если функция дифференцируема дважды в интервале и в нём (), то является выпуклой вниз (соответственно выпуклой вверх) в интервале .

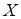Необходимое условие точки перегиба. Если 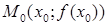- точка перегиба функции 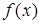, то либо 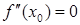, либо 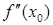не существует (рис. б, в). Следовательно, абсциссы точек перегиба нужно искать в тех значениях x, при которых вторая производная либо равна нулю, либо не существует.

Достаточное условие точки перегиба. Пусть функция 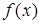имеет производную (может быть бесконечную) в точке , существует вторая производная в проколотой окрестности точки и либо 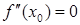, либо 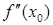не существует. Тогда если при переходе через 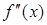меняет знак, то 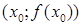является точкой перегиба.