Примеры решения типовых задач. Пример 1. Найти наибольшее и наименьшее значения на отрезке

Пример 1. Найти наибольшее и наименьшее значения на отрезке .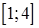

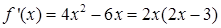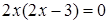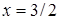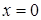Решение. , причем производная определена всюду, критических точек нет. Чтобы найти стационарные точки, приравниваем производную к нулю: . Итак, и – стационарные точки. При этом 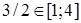, а , поэтому последняя точка нас не интересует. Вычисляем значения исходной функции в выбранной точке и на концах отрезка: ; ; .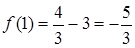

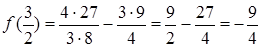Сравнивая значения, получаем: , .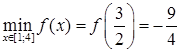

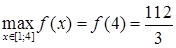Пример 2. Найти наибольшее и наименьшее значения 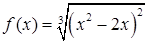в интервале .

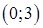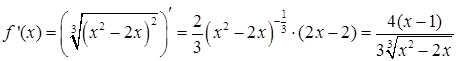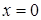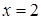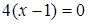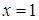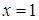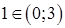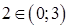Решение. , причем производная не существует при и . Эти точки являются критическими. Чтобы найти стационарные точки, приравниваем производную к нулю: , т.е. . Итак, - стационарная точка. При этом и , а 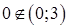, поэтому последняя точка нас не интересует. Вычисляем значения исходной функции в выбранных точках:

, .

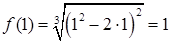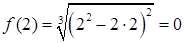Находим предельные значения функции на границах интервала:

;

.

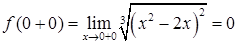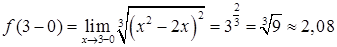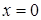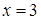Эти значения в точках и функция не достигает, поскольку эти точки не принадлежат интервалу .

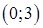Сравнивая 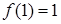, , 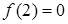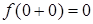и 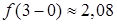, получаем 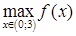не существует, .

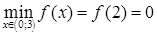При решении задач практического характера полезно пользоваться следующим фактом.

Пусть функция 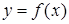определена на открытом числовом интервале 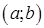и имеет на нем единственную стационарную точку . Если – точка локального максимума, то 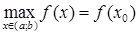; если - точка локального минимума, то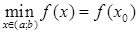

Пример 3. Предприятие выпускает некий товар в объеме, превосходящем 1 кг. Прибыль (в у.е.) зависит от объема выпущенного товара (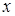) и определяются формулой 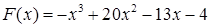. Найти объем производства товара, при котором прибыль будет максимальна.

Решение. В силу условий задачи функция, максимум которой нас интересует, определена на интервале 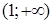. Найдем производную этой функции и приравняем к нулю: 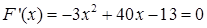. Решив квадратное уравнение, получим два корня: 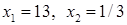. Очевидно, что условию задачи удовлетворяет только первое значение (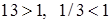). Сравнив знаки производной слева и справа от точки , получим, что это точка максимума. Находим максимальное значение на заданном интервале: .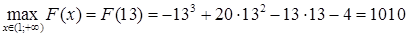

Итак, при объеме производства в 13 единиц прибыль будет максимальной и составит 1010 у.е.

Пример 4. Определить наибольшую площадь равнобедренного треугольника, вписанного в круг радиуса .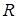

Решение. Пусть 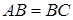и , тогда 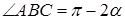, 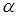– острый угол. Из теоремы синусов имеем

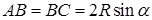, а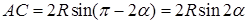

.

.

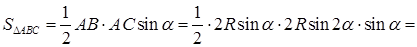
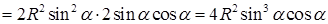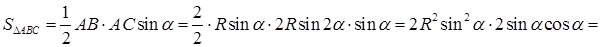
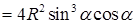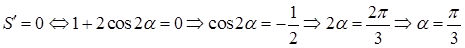– стационарная точка функции .

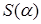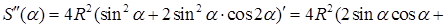
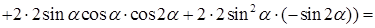
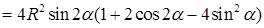
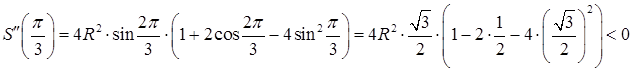
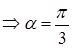– точка локального максимума, так как функция 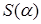непрерывна на 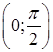и имеет единственную точку локального максимума, то в этой точке обязательно достигается наибольшее значение функции на этом интервале. Найдем 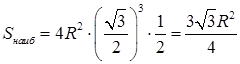(кв.ед.).

Задания для самостоятельной работы

n 68. Найти наибольшее и наименьшее значения функции на отрезке.

а) 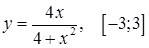;	б) ;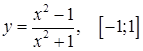
в) 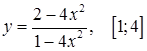;	г) ;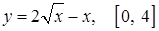
д) 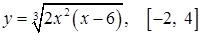;	е) ;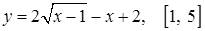
ж) 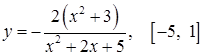;	з) ;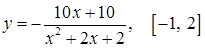
и) 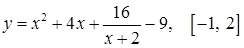;	к) .

Задача 69. Найти наибольшее и наименьшее значения на указанном промежутке.

а) 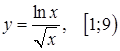;	б) ;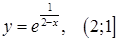
в) 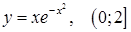;	г) ;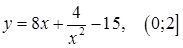
д) 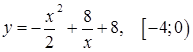;	е) ;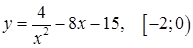
ж) 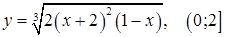;	з) ;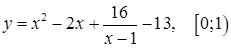
и) 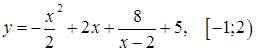;	к) .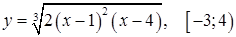

n 70. Решить задачу

а) Имеется 200 метров железной решетки, которой надо огородить с трех сторон площадку, примыкающую четвертой стороной к длинной каменной стене. Каковы должны быть размеры площадки, чтобы она имела наибольшую площадь?

б) Кровельщику надо сделать открытый желоб, поперечное сечение которого имеет форму равнобочной трапеции. Как дно, так и бока желоба имеют ширину 10 см. Какова должна быть ширина желоба наверху, чтобы он вмещал наибольшее возможное количество воды?

в) Консервная коробка цилиндрической формы с дном и крышкой должна вмещать V см в кубе. Каковы должны быть размеры коробки, чтобы на ее изготовление пошло наименьшее количество материала?

г) Бак без крышки с квадратным основанием должен вмещать V литров воды. Каковы должны быть размеры бака, чтобы на его изготовление было затрачено наименьшее количество материала?

д) Из квадратного листа жести со стороной а надо изготовить открытый сверху ящик. Для этой цели по углам листа вырезают равные квадраты и образовавшиеся края загибают сверху. Какого размера следует сделать вырезы, чтобы полученный ящик имел наибольшую вместимость?

е) Полотняный шатер объемом V имеет форму прямого кругового конуса. Каково должно быть отношение высоты конуса к радиусу основания, чтобы на шатер ушло наименьшее количество полотна?

ж) Из полосы жести шириной 60 см, требуется сделать открытый сверху желоб, поперечное сечение которого имеет форму равнобочной трапеции. Дно желоба должно иметь ширину 10 см. Каков должен быть угол, образуемый стенками желоба с дном, чтобы он вмещал наибольшее количество воды?

з) Стрела прогиба балки прямоугольного поперечного сечения обратно пропорциональна произведению ширины этого сечения на куб его высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром d, с наименьшей стрелой прогиба (наибольшей жесткости)?

и) Сопротивление балки прямоугольного поперечного сечения на изгиб пропорционально произведению ширины этого сечения на квадрат его высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром d, чтобы ее сопротивление на изгиб было наибольшим?

к) На верхнее основание прямого кругового цилиндра поставлен прямой конус с таким же основанием. Высота конуса равна радиусу основания. Сумма боковых поверхностей цилиндра и конуса равна 625 см. Когда объем тела, составленного цилиндром и конусом, будет наибольшим?