Устойчивость схемы Эйлера на модельной задаче

Для разностных схем, используемых в приближенном решении дифференциальных уравнений, естественно требовать выполнения аналогичного свойства устойчивости:

.

Оказывается, что свойство устойчивости разностных схем связано с их сходимостью. Например, исследуем устойчивость явной схемы Эйлера на примере решения модельного уравнения (3):

, отсюда

, т.е.

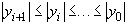, если ,

т.е. для устойчивости достаточно выполнения условий

и .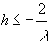

Таким образом, явная схема Эйлера условно устойчива, поскольку накладывается условие на шаг. Действительно, легко убедиться в том, что при большом шаге схема становится неустойчивой при . Пусть, например, , тогда

,

т.е. схема неустойчива.

Иначе обстоит дело с неявной схемой Эйлера. Рассмотрим ту же модельную

задачу:

,

следовательно,

,

и схема устойчива при для любого шага , поскольку .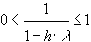

[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]

[Home|Кафедра|ПетрГУ]