 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейный интерполяционный сплайн
|
|
Пусть  - разбиение отрезка
- разбиение отрезка 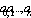 .
.
 ,
, 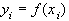 - заданные значения.
- заданные значения.
Сплайном первой степени называется:непрерывная на отрезке 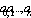 , линейная на каждом частичном промежутке
, линейная на каждом частичном промежутке  функция. Его обозначение
функция. Его обозначение  . Интерполяционным для данной функции
. Интерполяционным для данной функции 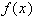 называется сплайн, удовлетворяющий условиям
называется сплайн, удовлетворяющий условиям 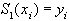 ,
,  .
.
График линейного интерполяционного сплайна  - это ломаная, проходящая через заданные точки.
- это ломаная, проходящая через заданные точки.
Пусть 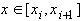 ,
,  . Выражение для сплайна
. Выражение для сплайна  на этом промежутке:
на этом промежутке:

Остаточный член:  .
.
Оценка остаточного члена зависит от дифференцируемых свойств функции 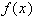 .
.
Пусть  . Обозначение
. Обозначение
 - колебание функции на
- колебание функции на 

Справедлива следующая лемма:
Лемма (вариант теоремы о среднем):
Пусть  . Если величины
. Если величины  одинакового знака, то существует
одинакового знака, то существует  такое, что
такое, что

С помощью этой леммы доказывается следующая теорема об оценке остаточного члена линейного интерполяционного сплайна.
Дата публикования: 2014-11-18; Прочитано: 895 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
