 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пусть требуется найти решение следующей системы линейных алгебраических уравнений
|
|
 (45)
(45)
причем 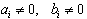 для всех
для всех 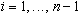 .
.
Матрица этой системы является трехдиагональной и имеет следующий вид:
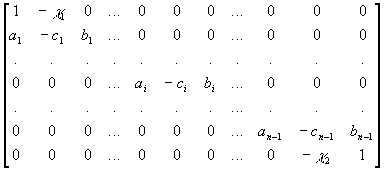
Это квадратная матрица размера 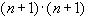 .
.
Предположим, что имеет место рекуррентное соотношение
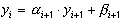 (46)
(46)
с неопределенными коэффициентами 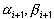 .
.
Из соотношений (46) и соотношений (45) находим:
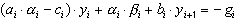
Сравнивая получаемое отсюда выражение для 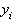 с формулами (46), получим рекуррентные формулы для прогоночных коэффициентов:
с формулами (46), получим рекуррентные формулы для прогоночных коэффициентов:
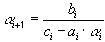 ,
, 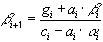 ,
, 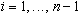 .
.
Начальные значения 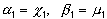 получим, сравнивая
получим, сравнивая 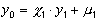 и (46) при
и (46) при 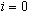 .
.
Для нахождения граничного значения 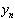 запишем систему уравнений:
запишем систему уравнений:
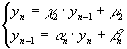
Исключая из системы 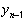 , получим
, получим
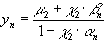 .
.
Итак, формально получен следующий алгоритм решения системы (45), который называется методом прогонки.
Сначала осуществляется прямая прогонка, т.е. находятся прогоночные коэффициенты
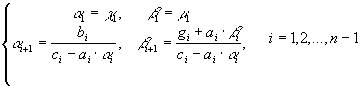 (47)
(47)
Затем осуществляется обратная прогонка по формулам
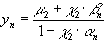 ,
, 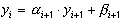 ,
,  (48)
(48)
[../О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]
[Home|Кафедра|ПетрГУ]
Дата публикования: 2014-11-18; Прочитано: 248 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
