Пример 6. Однако для матрицы размера 3×3 определитель строится сложнее:

.

Однако для матрицы размера 3×3 определитель строится сложнее:

(3)

Для простоты запоминания пользуются следующими схемами:

первые три суммы	последние три суммы

Схема называется правилом треугольников.

Модифицируем его, т.е. распрямим треугольники.

– схема Саррюса.

(4)

Если квадратная матрица имеет размер 4×4 и выше, то для вычисления ее определителя применяется правило Лапласа:

где: ,

(5)

т.е. детерминант матрицы 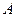равен сумме произведений элементов 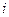-ой строки (или 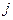-го столбца) на соответствующие алгебраические дополнения.

При этом – минор (определитель -го порядка), получающийся из матрицы 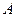вычеркиванием 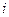-ой строки и 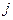-го столбца, – алгебраическое дополнение к элементу .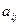

Заметим, что правило Лапласа позволяет определители 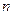-го порядка вычислять через определители -го порядка.