Пример. Рассмотрим в пространстве арифметических векторов с компонентами следующую систему из векторов:

Рассмотрим в пространстве арифметических векторов с 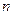компонентами следующую систему из 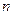векторов: . Эта система векторов является линейно независимой системой, так как непосредственно видно, что линейная комбинация 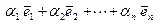равна нулевому вектору только в том случае, когда все коэффициенты равны нулю. Покажем, что любой арифметический вектор с 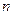компонентами может быть разложен по векторам .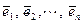

Действительно, справедливы следующие равенства:

.

Таким образом, система векторов образует базис в пространстве всех арифметических векторов с 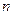компонентами, который принято называть каноническим базисом, а в соответствии с доказанной выше теоремой рассматриваемое в примере линейное пространство имеет размерность .

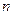Определение. Если некоторое непустое подмножество линейного пространства замкнуто относительно основных операций сложения и умножения на число исходного пространства, то оно называется подпространством.

Иначе говоря, если два любых вектора принадлежат подпространству, то их сумма 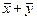и произведение на любое число также входят в подпространство.

Для всякого линейного пространства нулевой вектор образует подпространство, называемое нулевым. Отметим также, что нулевой вектор всегда входит в любое подпространство. По закону контрпозиции из того, что нулевой элемент не входит в некоторое подмножество, следует, что это подмножество не является подпространством. Общий прием построения подпространств основан на понятии линейной оболочки системы векторов.

Определение. Линейной оболочкой системы векторов

называется множество всех линейных комбинаций этих векторов .

Как следует из определения, линейная оболочка является подпространством исходного линейного пространства. Чтобы подчеркнуть алгоритм построения линейной оболочки, ее часто называют подпространством, порожденным векторами , или линейной оболочкой, натянутой на векторы .

Линейная оболочка является наименьшим подпространством, содержащим векторы . Действительно, это подпространство содержит векторы , из которых построена линейная оболочка . С другой стороны, всякое подпространство, содержащее векторы , обязано содержать и все линейные комбинации этих векторов.

Из доказанной выше теоремы о размерности пространства и его базисе следует, что если векторов линейно независимы, то линейная оболочка является подпространством с размерностью .

Построим далее решений однородной системы уравнений, полагая в общем решении вектор произвольных постоянных 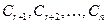равным векторам канонического базиса в пространстве арифметических векторов размерности :

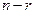Эти вектор – решения линейно независимы, так как линейно независимы векторы канонического базиса размерности 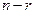, стоящие в нижних строках каждого из решений. Система вектор – столбцов решений 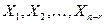называется фундаментальной системой решений однородной системы уравнений. Любая линейная комбинация этих решений

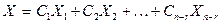
также является решением, так как по линейным свойствам матриц имеем:

=

= .

Таким образом, мы построили множество решений однородной системы уравнений в виде линейной оболочки , натянутой на фундаментальную систему решений. Так как решения 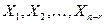представляют собой арифметические векторы длины и являются линейно независимыми, то размерность этой линейной оболочки равна 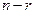. Другими словами, можно утверждать, что множество решений однородной системы с неизвестными, есть подпространство размерности 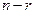пространства размерности .

Если мы возьмем любое решение однородной системы, то оно обязательно входит в линейную оболочку . Действительно, рассмотрим разность между и

решением 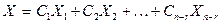из линейной оболочки .

Используя линейные свойства матриц, получим:

.

Так как любая однородная система имеет тривиальное решение, то

и

при некоторых значениях произвольных постоянных.

Таким образом, любое решение однородной системы уравнений всегда может быть представлено в виде линейной комбинации 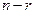произвольных постоянных и 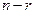фундаментальных решений, так что:

.

Если задана произвольная неоднородная система , то для записи ее общего решения полезна следующая теорема.