Исследование и решение однородных систем уравнений

Однородная система всегда совместна, так как имеет нулевое (тривиальное) решение . В этом случае и в преобразованной матрице коэффициентов, и в преобразованной расширенной матрице всегда одинаковое число строк. Таким образом, всегда и всегда выполняется теорема Кронекера – Капелли.

Если дополнительно ранг матрицы коэффициентов равен числу неизвестных системы , то, учитывая выполнение всех условий следствия 1 из теоремы Кронекера – Капелли, тривиальное решение системы является единственным решением системы.

Если система линейных уравнений однородна и 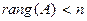, то ее множество решений бесконечно и зависит от 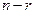произвольных постоянных 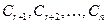. Среди бесконечного множества решений однородной системы всегда можно выделить ровно 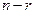линейно независимых решений размерности .

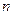Прежде чем построить эти решения приведем необходимые определения и теоремы, справедливые для любых линейных пространств.

Определение. Будем говорить, что линейное пространство имеет размерность 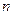и обозначать 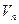или , если в этом линейном пространстве существует линейно независимая система из 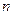векторов, а любая система из 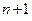вектора линейно зависима.

Другими словами, линейное пространство имеет размерность 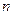, если наибольшее число линейно независимых векторов в этом пространстве равно .

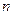Размерность пространства, состоящего из единственного нулевого элемента, считается равной нулю. Может случиться, что для любого сколь угодно большого числа 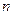в некотором линейном пространстве имеются 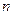линейно независимых векторов. Такие пространства называют бесконечномерными линейными пространствами. Например, таким пространством будет линейное пространство, состоящее из полиномов любой степени, которое имеет базис . Теория конечномерных линейных пространств выделяется из общей теории путем постулирования дополнительной аксиомы размерности.

Например, для двумерного пространства выделяющей аксиомой будет следующая: « Любая тройка векторов в линейном пространстве линейно зависима, но в пространстве существуют два линейно независимых вектора.

Размерность любого конечномерного пространства равна числу векторов базиса этого пространства, что устанавливается следующей теоремой.

Теорема (о размерности пространства и его базисе). Для того чтобы линейное пространство имело размерность 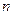, необходимо и достаточно, чтобы любая линейно независимая система из 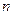векторов являлась базисом этого пространства.