Системы линейных уравнений. Основные понятия и определения

Основные понятия и определения

Определение 6.1. Системой m линейных уравнений с n неизвестными называется система вида:

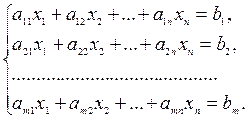(1)

Здесь x ₁, …, x_n – неизвестные (или переменные), числа а_ij – коэффициенты при неизвестных, i – номер уравнения, j – номер неизвестного, b ₁, …, b_m – свободные члены.

Короче систему (1) можно записать в виде: 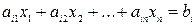, где i = 1, 2, …, m.

С каждой системой вида (1) связаны следующие матрицы: А – основная матрица системы, составленная из коэффициентов при неизвестных; В – матрица-столбец свободных членов, Х – матрица-столбец неизвестных; (А | B) – расширенная матрица системы.

А_{m ´ n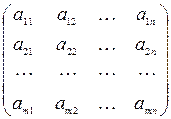} = , B_{m ´1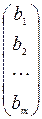} = , X_{n ´1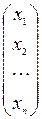} = , (А | B) _{m ´( n + 1)} = .

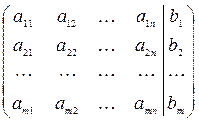Из определения 6.1 видно, что матрицы А и Х согласованы, следовательно можно найти их произведение:

А × Х = × = .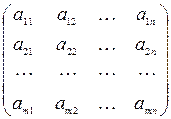

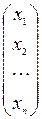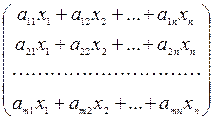Если воспользоваться определением 3.4 равенства матриц, то равенство

А × Х = В (2)

записывается в виде системы линейных уравнений (1).

Определение 6.2. Уравнение (2) называют матричной формой записи системы (1).

Определение 6.3. Решением системы линейных уравнений (1) называется любой упорядоченный набор (кортеж, вектор) а = (a₁, a₂, …, a _n) из чисел, который при подстановке в систему каждое уравнение обращает в верное равенство.

Таким образом, если а = (a₁, a₂, …, a _n) решение системы, то следующие равенства верны:

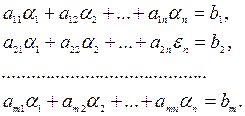
Определение 6.4. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Определение 6.5. Система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Определение 6.6. Две системы линейных уравнений называются равносильными, если множества их решений совпадают.

То есть, если упорядоченный набор чисел а = (a₁, a₂, …, a _n) является решением первой системы, то он является решением второй и наоборот, если упорядоченный набор чисел является решением второй системы, то он является решением первой системы.