Динамическое действие нагрузок на конструкции при работе механизмов подъема, передвижения, вращения, и изменения вылета кранов

Механизм подъема. Динамическое воздействие груза на кон­струкцию имеет место как при движении висящего на канатах груза, так и в процессе натягивания канатов, когда груз еще не оторвался от основания.

Рис. 8.6. Положения конца стрелы при перемещении

В теоретическом решении будем пренебрегать массой каната, что вполне допустимо при высотах подъема, характерных для кранов, а также изменением его длины за время развития макси­мальных динамических перемещений, что оправдано при тех скоростях подъема, которые практически имеют место. При рис- смотрении колебаний конструкции и груза будем пренебрегать упругостью механизма и влиянием высокочастотных колебаний натяжений каната на режим работы тихоходных крановых двига­телей. В начальный момент, когда усилие в канатах возрастает от нуля до значения, соответ­ствующего статическому натя­жению от веса груза, происхо­дит некоторое снижение часто­ты вращения двигателя, зави­сящее от его характеристики. Это уменьшает динамическое воздействие груза на конструк­цию, т. е. отсутствие учета обратной связи в виде влия­ния скорости нарастания на­грузки на режим работы двига­теля увеличивает запас надеж­ности. При рассмотрении динами­ческих перемещений металличе-, ской конструкции будем при¹ нимать ее за систему с одной степенью свободы с приведен­ной массой ш_м и приведенной жесткостью с_м. Такая простая схема дает решения с достаточ­ной точностью в очень многих случаях. Точку приведения принимаем там, где приложена нагрузка от веса груза на канатах (включая грузозахват) Q_K. Деформацией основания, на котором лежит груз, при его подъеме пренебрегаем, что в обычных условиях вполне допустимо. Также пренебрегаем влиянием затухания колебаний на уменьшение наибольшего динамического перемещения конструкций, что мо­жет иметь практическое значение лишь при полиспастах кратности более трех. При динамике подъема есть случаи, когда конструк­цию надо принимать за систему с двумя степенями свободы. На­пример, у башенных кранов в процессе колебаний конструкций горизонтальными перемещениями пяты стрелы, прикрепленной к башне, пренебрегать нельзя (рис. 8.6).

Рассмотрим упрощенную методику динамического расчета при подъеме груза. Результаты натурных тензометрических испытаний мостовых, портальных и других типов кранов дают возмож­ных. ib принять следующие допущения: усилия в канатах в про­цессе их натягивания, пока груз еще лежит на основании, воз­растают линейно, т. е, линейно возрастает нагрузка, приложенная к конструкции; после отрыва груза от основания, а также после торможения висящего на канатах груза, поскольку колебания второй частоты в конструкции малозаметны, а в канатах хотя и заметны, но быстро затухают, груз совместно с конструкцией совершает колебания той же частоты, т. е, канат по сравнению с конструкцией является весьма жестким.

Если "принять для динамического коэффициента значение по формуле (8.20), где в соответствии со сделанными допущениями:

; (8.25)

(где v — скорость подъема), то получим, что

где

(8.26)

Однако практически время Т оказывается то меньше, то больше, чем определенное по формуле (8.25), и более правиль­ным является определение величины по формуле

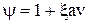, (8.27)

где значения причем = 2, когда отрыв груза от основания производится с полной скоростью, что является наруше­нием условий эксплуатации и может рассматриваться лишь как особая нагрузка. Для отдельных групп кранов зна­чение устанавливается на основании дополнительных исследова­ний, зависящих от способа запуска подъемного механизма (не­регулируемый, регулируемый или автоматический). Если такие данные отсутствуют, то можно принимать для кранов общего наз­начения = 1,5. Чем больше грузоподъемность крана, тем меньше скорость подъема, избыточный момент двигателя (тормоза) и ча­стота его вращения, а потому и силы инерции при разго­нах (торможениях). При этом начинает проявляться демпфиру­ющее влияние потерь в полиспастной системе, которые в упро­щенной методике динамического расчета не учитываются, так как имеют для малых и средних грузоподъемностей при обычных для них скоростях небольшое значение.

Для предварительных расчетов значение динамического коэф­фициента конструкции можно также принимать равным значению его для каната при абсолютно жесткой конструкции, Тогда в соот­ветствии с решением дифференциальных.. уравнений движения конструкций при работе механизма подъема

(8.28)

Значение будет наибольшим при крайнем положении тележка на крановом мосту, при положении тележки у опоры козлового крана и мостового перегружателя и во всех других случаях» когда деформациями конструкций у_Ст можно пренебречь. При этом механизм подъема и рама тележки будут испытывать наи­большую нагрузку. Расчетным будет этот случай и для некоторых элементов металлических конструкций, например для опорных частей кранов.

Если действующая на кран вертикальная сила Р_в кроме вер­тикальных 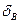вызывает также и горизонтальные перемещения, что имеет место, например, в стреловых кранах, то на конец стрелы будет действовать горизонтальная инерционная сила (рис. 8.6) P_t. = m_M . Если учесть, что под влиянием этой силы масса у корня стрелы m_к получает перемещение, например в.результате прогиба колонны крана, данная упругая система будет иметь две степени свободы. Рассмотрим приближенное решение вопроса, когда перемещением массы у корня стрелы можно пренебречь и рас­сматривать упругую систему как имеющую одну степень свободы. При этом перемещение массы m_м на конце стрелы будет характе­ризоваться ее углом поворота.

Ускорение в вертикальной плоскости /_в = P/( _i + m_г). По­скольку перемещения б_г и 6_В достигаются в одно и то же время, ускорение в горизонтальной плоскости /',, = 6_г/„/6_м т. е.

(8.29)

Предполагается, что масса груза на гибком подвесе не оказы­вает влияния на значение Р_т, т. е. период поперечных- колебаний груза при наименьшей высоте его подвеса h (м)

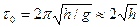(8.30)

значительно больше периода свободных колебаний конструкции как в вертикальной, так и в горизонтальной плоскости. В боль­шинстве практических случаев т₀ > Зт, что позволяет пренебречь влиянием второй частоты и пользоваться формулой (8.29).

Рассмотрим торможение опускающегося груаа. При упрощен­ном рассмотрении торможения опускающегося груза его можно принять мгновенным. Тогда вся кинетическая энергия груза V_H перейдет в потенциальную энергию каната U₁ и конструкции U_% и последняя будет испытывать наибольшую нагрузку. Так как

; ,

тогда ; U₂ = , а Р_д/ f _д = , поэтому .

Тогда

и

Максимальное усилие

, (8.31)

т. е.

, (8.32)

где

. (8.ЗЗ)

Коэффициента, определенный по формуле (8.33), всегда меньше, чем определенный по формуле (8.26), если пред­ставляет собой только упругое удлинение каната (мостовые, козловые и другие краны, где канат, сходящий с барабана, висит вертикально). Это очевидно из энергетических соображений. При мгновенном торможении опускающегося груза его кинети­ческая энергия переходит в потенциальную энергию конструкции и канатов. При отрыве груза от основания в потенциальную энер­гию конструкции и канатов кроме кинетической энергии груза переходит еще кинетическая энергия массы конструкции, по­скольку к моменту отрыва груза от основания конструкция под влиянием натягивающихся канатов деформируется и масса ее обладает скоростью. Поэтому при упрощенном рассмотрении задачи (мгновенное торможение, пренебрежение затуханием ко­лебаний и т. п.), если скорости подъема и спуска одинаковы, дина­мический коэффициент при подъеме с основания больше, чем при торможении во время спуска. При двигателях постоянного тока при торможении опускающегося груза они будут оказывать тормозящее действие и снижать динамические нагрузки.

Механизм передвижения. При передвижениях крана динамиче­ские воздействия на его конструкцию возникают как в периоды разгона и торможения, так и при установившемся движении в результате перемещения крана по неровному пути, например при проходе через неровные стыки рельсов и т. п.

Поскольку жесткость механизма высока по сравнению с же­сткостью конструкции и тем более гибкого подвеса груза, до­пущение об абсолютно жестком механизме заметно не влияет на результаты теоретического исследования. Самая низкая частота свободных колебаний в системе привода значительно выше, чем частота колебаний большинства крановых конструкций. В от­дельных случаях, например при длинных трубчатых трансмиссион­ных валах механизмов передвижения крановых мостов, может оказаться целесообразным учесть упругость механизма, хотя все же поправка к значениям динамических перемещений (напряже­ний) в конструкции будет невелика.

При рассмотрении динамических перемещений конструкции с расположенными на ней механизмами принимаем ее за систему с одной степенью свободы с приведенной массой т_м и приведенной жесткостью в горизонтальной плоскости с_м. Точку приведения будем считать совпадающей с местом, где приложена нагрузка от груза. Колебания конструкции будем рассматривать в гори­зонтальной плоскости, считая их независимыми от колебаний в вертикальной плоскости. Груз может быть подвешен к кон- струкции на канатах — система с двумя степенями свободы {колебание массы т_м и груза) пли па жесткой подвеске — система с одной степенью свободы, Теоретические решения, основанные на рассмотрении дифференциальных уравнений движения кон­струкции и груза, имеются в рекомендуемой литературе.

Рассмотрим упрощенную методику динамического расчета механизма передвижения. При разгонах и торможениях кон­струкции, как правило, находятся в условиях кратковременного действия нагрузки (см. рис. 8.4). Так как при передвижении кранов обычно груз находится в положении, близком к высшему, то можно гибкий подвес уподобить жесткому, что несколько преувеличит влияние груза на горизонтальные силы инерции. При резком разгоне или торможении наибольшее усилие, при­ложенное к приведенной массе конструкции т_ш

, (8.34)

а при плавном разгоне или торможении —

, (8.35)

где т_ш — приведенная масса крана; — среднее

ускорение, определяемое средним пусковым моментом двигателя М_ДВ (расчетным моментом тормоза), при котором тяговое усилие, создающее ускорение,,

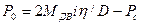, (8.З6)

гдеi — передаточное число механизма; — КПД механизма; D — диаметр ходового колеса;Р ,. — усилие, расходуемое на пре­одоление статических сопротивлений; М — масса всей движу­щейся конструкции крана (тележки); в тех случаях, когда инер­цией вращающихся частей привода пренебречь нельзя, к значению массы т_т должно быть добавлено значение эквивалентной массы вращающихся частей привода , где J — момент инерции всех вращающихся частей привода, отнесенный к валу двигателя; — угловая скорость двигателя, соответствующая скорости передвижения крана (тележки) v. Наибольшее расчетное значение ускорения, определяемое максимальным моментом дви­гателя (тормоза), ограничивается условиями сцепления колес с рельсами

(8.37)

где = 0,10 0.20 — коэффициент сцепления (меньшее значе­ние — при смазанных или влажных рельсах, большее — при сухих), у кранов, снабженных песочницами, ₀ достигает 0,25; N_ДВ и N — давление на приводные колеса (включая влияние горизонтальных инерционных сил и ветра) и полное давление на все колеса, Кроме того, следует произвести проверку при пуске (торможении) и максимальном моменте двигателя (тормоза) без учета упругих колебаний конструкции, при которых должно

выполняться условие

, (8.38)

где j_шах — максимальное ускорение крана {см. формулу (8.37) 1; — давление на приводные колеса крана. Случай, когда для определения силы в формулу (8.34) следует подставлять не j, а j_шах, можно рассматривать лишь как особую нагрузку. Горизонтальные силы инерции при передвижении тележек по кра­нам или рельсовым путям

, (8.39)

где j_max — максимальное ускорение тележки; N_пр — давление на приводные. колеса тележки; m _T — масса тележки. Следует отметить, что при рассмотрении работы механизмов передвижения уточнение динамических расчетов имеет меньшее значение, чем при рассмотрении работы механизмов подъема, так как в расчетах используются средние значения .

Вертикальные динамические нагрузки, возникающие из-за неровности пути (толчка) при передвижении крана (тележки, поворотной части), учитываются коэффициентом толчков k,. На коэффициент толчков следует умножать как вес конструкции, так и вес груза, имея в виду минимальную высоту его подвеса, При расчетах на сопротивление усталости, .

При рассмотрении горизонтальных колебаний порталов, воз­никающих от действия горизонтальных инерционных сил, ветра и сейсмических нагрузок, нужны значения периодов их свободных колебаний . Будем рассматривать портал как одномассовую систему, масса которой m состоит из массы тележки (поворотного крана), расположенной на верхнем строении, массы верхнего строения, поскольку продольными колебаниями его пренебрегаем, и 1/3 массы опор. Для такого случая

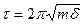(8.40)

где — горизонтальное смещение верхнего строения портала (массы т) от единичной горизонтальной силы, поскольку же­сткость с = 1/ . При двух неподвижных опорах (рис. 8.7,а)

;

; (8.41)

При одной неподвижной (рис. 8.7, б), а второй — шарнирной

, (8.42)

где — изгибающий момент от силы, равной единице; k = hJ/(l ). Если размеры сечения опоры изменяются по высоте, можно для Уj принимать среднее значение из значений моментов инерции верхнего и нижнего сечений.

Механизм вращения. В периоды разгона и торможения меха­низма вращения динамические воздействия на его конструкцию (стрелу) возникают от раскачивающегося на канатах груза и вра­щающихся масс конструкции. Если рассматривать колебания груза в плоскости, перпендикулярной к стреле, пренебрегая отклонением груза вследствие действия центробежной и кориоли- совой сил инерции, что, как правило, допустимо, и рассматривать стрелу как двухмассовую систему с приведенными массами на конце m _м и в корне стрелы, то для случая вращения крана можно использовать все основные выводы, сделанные при рассмотрении динамики механизма передвижения.

Рис. 8.7. Схема горизонтального смещения портала б: при двух неподвижных опорах (а); при одной неподвижной (жесткой) и другой подвижной (гибкой) опоре (б)

Исследования раскачивания груза на канатах у поворотных кранов позволили установить следующие основные положения,

6) Углы отклонения грузового каната зависят от движения точки подвеса груза, которое происходит в соответствии с эксплу­атационными режимами работы кранов. Основным движением, определяющим характер колебаний груза, обычно является по­ворот крана.

7) Наибольшие динамические нагрузки возникают при макси­мальных грузах и минимальных длинах их подвески h.

8) При чередовании пусков и торможений и одновременном совмещении отдельных движений крана качания груза на канатах, вызванные отдельными движениями (в силу медленного затухания качаний груза и благодаря приблизительному сохранению пло­скости качания груза при повороте), могут совпадать и по напра­влению, и по фазе; амплитуды качаний будут при этом алгебра­ически складываться.

4.Угол и в связи с этим усилие Р_г, передающееся на конец стрелы (рис. 8.8), в значительной мере зависят от режима экс­плуатации крана.

Рис. 8.8. Схема сил, дей­ствующих на конец стрелы

Рассмотрим упрощенную методику определения отклонения грузовых канатов. Отклонение груза от вертикали и его раскачи­вание на канатах возникают под действием: сил инерции массы груза при разгонах и торможениях механизмов вращения; давле­ния ветра на груз Р_в; качки (плавучие краны). При отклонении канатов на угол а возникает горизонтальная сила Р_г — Q_K tg а, которая через усилие в канатах передается на конец стрелы и мо­жет быть направлена различно по отношению к плоскости стрелы (рис. 8.8). Если предположить, что инерционные силы от массы груза на канатах действуют статически, то они будут равны: "касательная сила инерции при повороте, действующая перпен­дикулярно к плоскости стрелы,

; (8.43)

центробежная сила инерции при повороте, действующая в плоскости стрелы,

; (8.44)

сила инерции при изменении вылета, действующая в плоскости стрелы,

, (8.45)

сила инерции при передвижении крана, могущая быть направленной любым образом по отношению к пло­скости стрелы,

, (8.46)

где п — частота вращения крана, об/мин; v„_t v_n — скорости изменения вылета и передвижения крана, м/с; t_K, t_m t_a — время пуска (торможения) соответствующих механизмов.

Если при резком пуске или торможении какого-либо механизма (см. рис. 8.4), то соответствующую силу 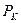, Р_И или Р_П надо считать вдвое большей. Если условие t_x > т/2 не выпол­няется, то в расчет следует вводить силы P _к „ и , где < 2. Если пуск или торможение механизма производится плавно с нарастанием момента в течение времени Т, то значения ij; определяются по формуле (8.19).

Таким образом, отклонение грузовых канатов может проис­ходить под влиянием сил Р_и, Р„ и Р_п, возникающих в условиях пуска или торможения механизмов, о учетом их динамического характера, и сил Р_п и Р_п. При этом в силу медленного затухания качаний груза и благодаря сохранению плоскости качания груза при повороте крана амплитуды качаний, вызванных отдельными силами, могут арифметически складываться. Случай суммирова­ния максимальных амплитуд качаний всех указанных выше сил при резких пусках и торможениях надо признать безусловно нереальным. Действительные максимальные углы составляют ¹/₃— 1/2» от максимально возможных расчетных углов. Вопрос о воз­можных совмещениях движений и максимальных углах отклонения грузовых канатов надлежит решать для отдельных групп кранов по данным их эксплуатации. В периоды разгона или тор­можения механизма вращения динамические воздействия на его конструкцию возникают не только от раскачивающегося на кана­тах груза, но и от вращающихся масс поворотной части.

Механизм изменения вылета. Если изменение вылета осуще­ствляется путем перемещения тележки по стреле, инерционные силы, действующие на тележку, определяются, как при передви­жении. Если изменение вылета осуществляется путем качательных движений стрелы, учет влияния раскачивания груза обычно производится совместно с раскачиванием, вызываемым вращением. Исследования инерционных сил при изменении вылета у кранов подтвердили отсутствие динамической связи между раскачиванием груза и упругими колебаниями стрелы, показали, что решающее влияние на динамические напряжения имеют колебания а часто­той низшего тона и интенсивность эксплуатации (наложение колебаний, возникающих при разгонах и торможениях). При нормальных торможениях и пусках силы инерции масо стрело­вого устройства определяются исходя из времени торможения или пуска. При резких торможениях для механизмов среднего и тяжелого режимов работы можно принимать динамический коэффициент для касательных инерционных сил масо стрелового устройства равным двум.

При рассмотрении динамики металлических конструкций при совместной работе нескольких механизмов очевидно, что принятие наибольших динамических нагрузок в виде суммы наибольших динамических нагрузок, возникающих при работе каждого из механизмов, будет завышать действительные напряжения в кон­струкциях. Степень завышения будет зависеть от типа крана, его параметров и интенсивности его эксплуатации.