Определение динамического воздействия на одномассовую систему при нагрузке, возрастающей по линейному закону, приложенной мгновенно и кратковременно

Рассмотрим влияние различных способов приложения сил, характерных для конструкций подъемно-транспортных машин, на движение системы с одной степенью свободы. При этом будем пренебрегать диссипативными силами, т. е. силами вредных сопротивлений.

Нагрузка, возрастающая по линейному закону. Пусть на массу т_м находившуюся в равновесии, подействовала нагрузка, возрастающая в течение времени Т до наибольшего значения Q по линейному закону (рис. 8.2, а).

1. При t с Т дифференциальное уравнение колебаний массы будет m_uy" + су = Qt/T, откуда

y" + p²y - Qt/(m_MT ), (8.6)

где с — жесткость связи (конструкции), с = Q/y_CT; у_{с т} —стати­ческое перемещение (прогиб) от действия нагрузки Q; р — круго­вая частота свободных колебаний системы, т. е. число колебаний в 2 п секунд, . Общее решение уравнения (8.6) за­пишем в форме

у = A sin pt + В cos pi + Qt/(p²m_MT), (8.7)

или

у = A sin pt + В cos pt + y_clt/T. (8,8)

При t = 0, y = 0 и y' = 0 и из выражения (8.8) найдем: ,

B=0, откуда

у = y_CT(t-sin pt/p)/T; (8.9)

у' = Уст (1 -cos pt)/T (8.10)

При t = Т из выражений (8.9) и (8.10) получим:

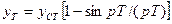(8.11)

, (8.11)

Из выражения (8,10) видно, что в течение всего промежутка времени i Т скорость перемещения массы m _м положительна (cos pt 1). При t= T у'_Т 0 (8.12), т. е. к моменту прекра­щения нарастания нагрузки масса обладает запасом кинетической энергии, который будет израсходован на дополнительную де­формацию системы. Таким образом, наибольшее перемещение система будет иметь при t > Т.

2. При f Т дифференциальное уравнение колебаний массы будет т_шу" + су = Q, откуда

. (8.13)

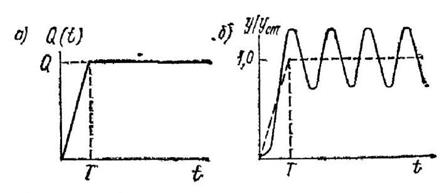
Рис. 8.2. Зависимость силового воздействия (а)и соответствующего ему перемещения массы (б)от вре­мени t

Общее решение уравнения (8.13) запишем в форме

у - С sin р (t — Т) + D cos р (t — Т) + (8.14) поскольку Q/(p²m_M) = ,

Подставляя в решение (8.14) t =Т и учитывая выражения (8.11) и (8.12), получим:

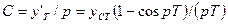. ( 8.15)

Подставим значения С и D из (8.15) в (8.14). Тогда

=

= =

= (8.16)

Так как период колебаний

, (8.17)

то, подставляя его значение в выражение (8.16), найдем

, (8.18)

Наибольшее значение перемещения

имеет место при , причем знак у единицы должен быть взят обратным знаку .

Отношение максимальных значений перемещений, усилий или вызываемых ими напряжений, возникающих в конструкции в ре­зультате динамического действия сил, к значениям, возникающим от статического приложения этих же сил, называется динамиче­ским коэффициентом.

В данном случае динамический коэффициент

Изменения коэффициента нарастания нагрузки k_H в зависи­мости от отношения 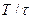представлены на рис. 8.3 штриховой линией.

При ; ; при ;

Для практического применения изменение коэффициента на­растания нагрузки , при T > 0,5 принимается по огибающей кривой, показанной на рис. 8.3 сплошной линией.

(8.20)

Как видно, при T / = 6,5 . Это значит, что, если период развития нагрузки T более чем в 6,5 раз превышает период свободных колебаний системы, динамическим влиянием нагрузки на систему можно пренебречь (с точностью до 5 %). На рис. 8.2, б показано перемещение массы т_ы в процессе колебаний для t T по уравнению (8.9) и для t < T по уравнению (8.18). Колебания происходят вокруг статического отклонения системы (штриховая линия), которое для t < T равномерно возрастает, а для t > T остается постоянным и равным .

Нагрузка, приложенная мгновенно. Такая нагрузка есть ча­стный случай нагрузки, возрастающей по линейному закону, при . Колебания происходят около положения статического равновесия [см. формулу (8.18)], и = 2у_CT.

Нагрузка, приложенная кратковременно. Пусть к массе m _м, находившейся в равновесии, была приложена мгновенно на­грузка. которая по истечении времени t ₁ так же внезапно была снята (рис. 8.4). Если , то наибольшее перемещение достигнет значения двойного статического, т. е. в этом случае независимо от значения . Если , то . Если t₁ < / 4, то во время действия нагрузки деформация не достигнет значения, получающегося при статическом нагружении.

Круговая частота р и период [см. формулу (8.17)) свобод­ных колебаний. Эта параметры являются основными динамиче­скими характеристиками конструкций. Круговая частота

, (8.21)

где m _м —действительная масса в одномассовой системе и при­веденная в многомассовой, совершающей одно из главных коле­баний; с действительная или приведенная жесткость кон­струкции.

Рис. 8.3. Зависимость коэффициента на­растания нагрузки k_H от Т/т

Рис. 8.4. Схема внезап­ного действия нагрузки на конструкцию

Техническая частота равна

n = 60р/(2 ), ' (8.22)

т. е. числу колебаний в минуту.

На частоту свободных колебаний можно воздействовать изме­нением массы и жесткости конструкций. Обычно динамически неудачные конструкции обладают малой частотой свободных колебаний. Для увеличения частоты колебаний конструкции нужно уменьшать ее массу. Однако возможностей заметного уменьшения массы конструкции, как правило, нет, поскольку всегда стремятся к созданию конструкций минимальной массы. Увеличения частоты в динамически неудачной конструкции обычно достигают за счет повышения ее жесткости. Жесткость можно увеличивать, изменяя сечения элементов конструкции или ее геометрическую схему. Последний путь более рационален. Же­сткость повышается с увеличением высоты ферм и балок, при добавлении новых связей и т. п.

Затухание колебаний конструкций. Колебания, возникающие в периоды разгона и торможения, имеют важное значение. Стремление к снижению массы металлических конструкций кра­нов привело к тому, что были отмечены случаи создания таких конструкций, которые в результате обычных операций по разгону и торможению груза начинали совершать медленно затухающие колебания, мешающие нормальной эксплуатации кранов. Приэтом статические и динамические напряжения и прогибы у кон­струкций этих кранов находились в обычных допустимых пре­делах. Такие медленно затухающие колебания конструкций и груза в ряде случаев снижают производительность крана при совершении им достаточно точных сборочных работ и отражаются неблагоприятно на самочувствии крановщика, особенно если кабина совершает колебания большой амплитуды, например, когда у мостового крана она расположена в середине пролета.

Рис. 8.5. Схема затухания колебаний

Известно также, что на не­которых типах башенных кранов в результате дейст­вия колебаний крановщики испытывали тошноту и голо­вокружение.

Затухание упругих ко­лебаний конструкций проис­ходит по закону экспоненты (рис. 8.5). Первоначальная амплитуда колебаний , характеризующая динамическую жесткость металлической кон­струкции, по истечении времени t и совершения колеба­ний равна

(8.23)

где —логарифмический декремент затухания, равный разности логарифмов двух последовательных амплитуд у₁ > у₂, т. е. 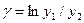; — коэффициент затухания, а п₀ — коэффициент сопротивления в уравнении колебаний . Из формулы (8.23) время затухания

(8.24)

Первоначальная амплитуда и допустимое время затуха­ния колебаний зависят от типа крана и условий его эксплуатации. Коэффициент затухания е может быть определен только экспери­ментальным путем. Для коробчатых крановых мостов (для H/l от 1/12 до 1/18) при t от 5 до 30 с. При колебаниях рабочего места с частотами до 5 Гц, что характерно для многих крановых конструкций, для организма человека не опасны уско­рения до 50 см/с². Если колебания конструкции или кабины чрезмерны, целесообразно не снижать напряжения в конструкции, увеличивая ее вес, а использовать гасители колебаний или вибро­изоляцию места крановщика.