Динамические расчетные схемы основных типов крановых конструкций и их приведенные массы

При работе отдельных механизмов крана силовое воздействие от двигателя или тормоза через систему привода передается на металлическую конструкцию, вызывая ее колебания и соответ­ствующие им напряжения. Результаты работ по различным во­просам динамики в краностроении показывают возможность све­дения действительных систем к упрощенным расчетным динами­ческим схемам. Колебания металлической конструкции можно рассматривать как колебания системы с конечным числом степеней свободы, т. е. с конечным числом независимых координат, опре­деляющих положение системы. Для этого распределенная масса конструкции заменяется одной или несколькими сосредоточен­ными приведенными массами, что зависит от схемы конструкции и положения точек, в которые приводятся массы. При этом следует стремиться к получению системы с минимальным числом степеней свободы. При рассмотрении колебаний, поскольку определяется наибольшее воздействие, имеющее место при первых колебаниях, можно пренебрегать силами неупругого сопротивления (затуха­нием колебаний). Жесткость валив несоизмерима с жесткостью канатных систем и металлических конструкций. Поэтому без сни­жения практической точности расчетов металлических конструк­ций упругость жестких передач привода можно не учитывать, что подтверждают экспериментальные тензометрические исследо­вания механизмов подъема, передвижения и вращения ряда кра­нов. Как показывают тензометр ические исследования крановых конструкций, уже колебания второй частоты затухают быстро. Поэтому практически в большинстве случаев достаточно огра­ничиться рассмотрением только основной низшей частоты.

При замене распределенной массы конструкции сосредоточен­ными массами исходят из динамической эквивалентности обеих систем, т.е. из сохранения максимальных значений кинетической и потенциальной энергии конструкции в процессе ее свободных колебаний.

В любом сечении балки, совершающей свободные колебания какой-либо частоты, на расстоянии x от конца ее перемещение , где f(x) — ордината прогиба в процессе колебаний; p — частота; — начальная фаза колебаний. Ско­рости перемещения:

а ;

Максимальное значение кинетической энергии для балки с рас­пределенной массой т будет равно

Заменим распределенную массу т несколькими сосредоточен­ными массами m. Таким образом,

(8.1)

Кроме того, общая масса балки должна сохраниться неизмен­ной, т.е.

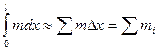(8.2)

В качестве примера рассмотрим определение приведенной массы для балки со свободно опертыми концами с равномерно распределенной по длине массой т, считая балку системой с одной степенью свободы. Примем уравнение прогиба балки от сосредо­точенной силы, равной единице в середине пролета, в виде синусо­иды, что широко используется при решении задач о колебаниях и прочности конструкций: , где 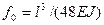. Из условия (8,1)

, (8.3)

откуда m_M/ml2. Точное решение дает значение m _м — 0,493ml. Из условия (8.2) очевидно, что на опорах будут сосредоточены массы m ₀ = 0,25 ml (рис. 8.1).

Если двухопорная балка, например мостового крана, кроме равномерно распределенной нагрузки q несет ряд сосредоточен­ных нагрузок G_i, то приведенная к середине пролета масса балки может быть определена исходя из формулы (8.1):

, (8.4)

Рис. 8.1. Схема определения при­веденной массы двухопорной балки

Где f_t (x) — ординаты прогиба от силы, равной единице в середине пролета, в тех сечениях балки, где приложены нагрузки G_t. При этом

где х 0,5 l — расстояние от опоры до точки приложения сосре­доточенной нагрузки ,. Если масса , расположена близко к опорам, то влиянием такой массы (например, кабина вблизи опоры моста) на значение в середине пролета можно пренеб­речь. Также можно пренебрегать влиянием базы тележки и рас­сматривать тележку как точечную массу. В более общем виде

, (8.5)

где — коэффициент приведения, a f_t (х) — прогиб в сечении, где приложена нагрузка G_t.

Если у двухопорной балки крана тележка стоит на расстоянии от опоры, то приведенная в эту точку распределенная масса балки (из услов ия равенства ее низшей частоты колебаний, ,

которая в динамических расчетах крановых конструкций имеет основное значение, и частоты заменяющей ее одномассовой системы с массой на расстоянии „ от опоры при колебаниях в вертикальной плоскости может определяться также по формуле (8.5), где, полагая р = р₀ и учи­тывая, 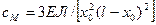, находим и .

Для консольной балки и для статически неопределимых балок приведенные массы могут быть вычислены аналогично по уравне­ниям (8.1) и (8.5). При этом для определения коэффициента а можно воспользоваться выражением кривой с формой изгиба, подходящей к получающейся при колебаниях, например статиче­ской упругой линией балки, или синусоидой. Так, для консольной балки с началом координат в заделке , а из условия (8.1)

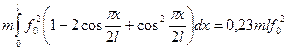
Отсюда приведенная масса на конце консоли аналогично формуле

. (8.3)

Для стержня с одним шарнирным и другим свободным концом (типа стрелы) из условия равенства кинетической энергий в про­цессесвободных колебаний равномерно распределенной массы стержня m и приведенной к его концу массы m _м находим, что

.

Отсюда т_м = ml! 3. Здесь — угловая скорость; v — окружная скорость на конце стержня,