Теоретическая часть. Есть такое числоe, без которого, пожалуй, не обходятся ни одни вычисления

Есть такое число e, без которого, пожалуй, не обходятся ни одни вычисления. Буква e совпадает с первой буквой фамилии выдающегося щвейцарского математика Леонарда Эйлера, который первым ввел это число в активное пользование. В мире математики существую гиперболические функции - гиперболические косинусы и синусы и пр. Называются они так из-за того, что для них выполняются тождества, похожие на тождества тригонометрических функций. Кроме того, они связаны с тригонометрическими функциями через мнимую единицу. Среди этих гиперболических функций есть гиперболический косинус, который выражается через полусумму экспонент с показателями разных знаков

.

Примечателен он тем, что в реальной жизни встречается невероятно часто. На рисунке среди прочих приведен график гиперболического косинуса.

Оказывается, что если взять нить или веревку и натянуть ее, но не очень сильно, так чтобы провисала, то полученная форма как раз и будет гиперболическим косинусом. Если же к каждой точке нити подвесить груз, сильно превышающей массу самой нити, то полученный профиль будет параболой - примеры таких конструкций - подвесные мосты. Форма, которую задает этот самый косинус, называется так же цепной линией.

Глядя на цепную линию, ее трудно отличить от параболы (или парабола пополам). На глаз их действительно не отличить. Но если честно посчитать аналитически, то получается гиперболический косинус или, как его называют, кошинус. Дело в том, что в малой окрестности нуля гиперболический косинус раскладывается в ряд Тейлора так:

т.е. главным членом разложения можно считать как раз параболу.

Оказалось, что если линию перевернуть, так, чтобы максимум оказался сверху - то эта форма будет тоже идеальной. Если по такому принципу строить арки, то они не обрушатся, т.к. силы во всех точках компенсируются. В древности прознали про эту особенность и "доисторические" арки, постро-енные таким образом не обрушились до сих пор.

Если строить мосты, выпуклыми вверх и совпадающие с гиперболическим косинусом, то они так же будут максимально прочными и долговечными.

Если задаться целью - строить крыши домов так, чтобы вода, попадая на них, как можно быстрее скатывалась вниз и не оказывала давления на крышу, то снова получается форма кошинуса. Примечательно то, что древние додумались до этого еще не зная об удивительном кошинусе. И построили эмпирические профили крыш, которые совпадают с аналитическими расчетами кошинуса.

Если сделать велосипед с квадратными колесами и задаться целью - как сделать дорогу так, чтобы велосипедиста не трясло вверх-вниз при езде, то снова получится периодический профиль, состоящий из кусочков гиперболических косинусов. Вот какой удивительный гиперболический косинус. Как же рассчитать аналитически эту функцию?

Начнем подходить к теме с воспоминаний. Обычный числовой ряд, состоит из чисел:

Все члены ряда – это ЧИСЛА.

Функциональный же ряд состоит из ФУНКЦИЙ:

Любой числовой ряд может или сходиться, или расходиться. Если числовой ряд сходится, то это значит, что сумма его членов равна некоторому конечному числу:

Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда в его области сходимости является некоторая функция , а именно sin(x). (Пока принимаем на веру все, что написано выше). Данный факт справедлив только для области сходимости, которую можно найти. Вне области сходимости с рядом может происходить все, что угодно. Но для рассмотренного функционального ряда область сходимости

Теперь вспоминаем школьный график синуса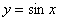

Если начертить график бесконечного многочлена 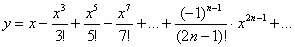, то получится та же самая синусоида! То есть, наш степенной ряд сходится к функции .

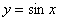А что значит вообще «сходится»? Если возьмем первые три члена ряда 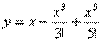и начертим график многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда: и начертить его график, то он будет с синусоидой практически совпадать. Чем больше членов ряда – тем лучше приближение. И, как уже отмечалось, график бесконечного многочлена – есть в точности синусоида. Иными словами, ряд сходится к функции 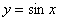при любом значении «икс».

Рассмотрим другой пример, табличное разложение арктангенса:

Область сходимости ряда:

Дело в том, что график бесконечного многочлена совпадает с графиком арктангенса только на отрезке (т.е. в области сходимости ряда):

Вне отрезка разложение арктангенса в ряд расходится.

Разложение функций в степенной ряд. Ряд Тейлора. Ряд Маклорена.

Критерий представимости функции рядом Тейлора.

Для любой бесконечно дифференцируемой в окрестности точки а функции f(х) имеет место формула Тейлора: f(x)= T_n(f(x),а)+R_n(f(x),а), где

T_n(f(x),а)=многочлен Тейлора порядка n в точке а, R_n(f(x),а) - остаточный член. Эта формула опубликована в 1715 английским математиком Б. Тейлором.

T_n(f(x),а) =

Если функция в некотором интервале раскладывается в степенной ряд по степеням , то это разложение единственно и задается формулой:
Т.е.

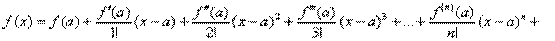(Вместо буквы «а» на практике часто можно встретить букву ).

В случае, если , этот ряд называется рядом Маклорена. (Колин Маклорен - шотландский священник, математик. В 19 лет занял по конкурсу кафедру профессора математики в Абердине, на которой и оставался в течение 5 лет).

На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда :

Разложение Маклорена также называют разложением Тейлора по степеням .

Запишем еще раз формулу Тейлора в развернутом виде

(R_n(x) - остаточный член формулы Тейлора).

Теорема (остаток в формуле Тейлора в форме Лагранжа). Пусть при всех существует -я производная . Тогда для любого существует точка , лежащая между и (то есть при ), такая что

(Остаточный член формулы Тейлора, представленный в таком виде, называется остаточным членом в форме Лагранжа.)

Остаточный член формулы Тейлора может быть записан в разных видах.

1. В форме Коши:

2. В форме Пеано:

при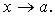

3. В интегральной форме:

Для примера выведем разложение экспоненциальной функции:

Как оно получилось? Запишем формулу Маклорена: Рассмотрим функцию , тогда:

Находим производные в точке ноль: первую производную, вторую производную, третью производную и т.д.

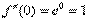
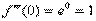
Т тортооооолллллл

Совершенно очевидно, что

Подставляем единицы в формулу Маклорена и получаем табличное разложение! Аналогично можно вывести некоторые другие табличные разложения (но, следует отметить, что не все функции разлагаются именно так).

Для гиперболического косинуса имеем разложение в ряд Тейлора по степеням

.

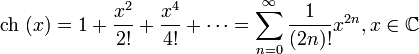Формула Тейлора применяется при приближенном подсчете значения функции в какой-либо точке, а остаточный член, посчитанный в этой точке показывает погрешность вычислений.

Поговорим немного об остаточном члене.

Теорема. Для того, чтобы бесконечно дифференцируемая в точке a функция f(x) являлась суммой составленного для нее ряда Тейлора, необходимо и до-статочно, чтобы остаточный член при п стремящемся к бесконечности, стремился бы к нулю.

Итак, для исследования вопроса о разложимости функции в ряд Тейлора нужно исследовать поведение его остаточного члена R_n(x) при n→∞. Стремится к нулю, то сумма ряда Тейлора равна значению функции в точке

x₀, то есть f(x₀). Если же R_n(x₀) не стремится к нулю, то ряд Тейлора либо расходится, либо его сумма при x=x₀ не совпадает со значением функции в данной точке x₀.